


在这个 C++ 程序中,我们必须生成多达 n 项的斐波那契数列。
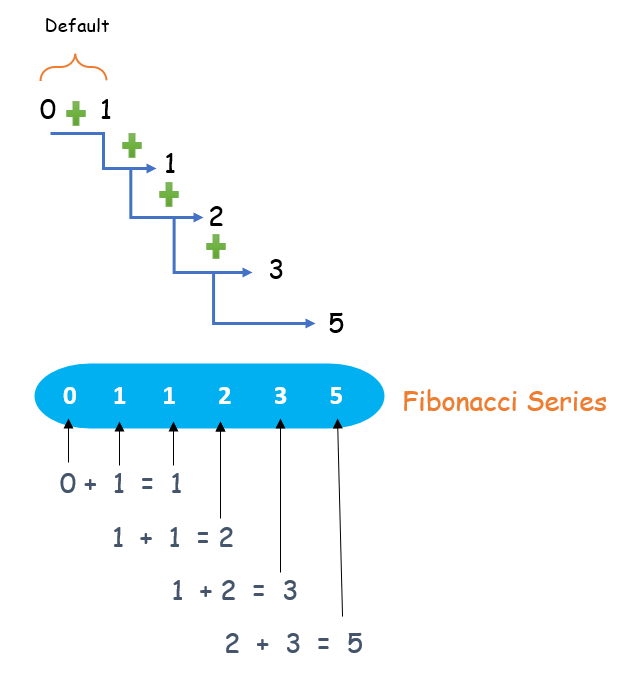
斐波那契数列是一个整数序列,其中除前两个数之外的每个数都是前两个数之和。前两个数手动设置为 0 和 1。序列中所有其余的数都是通过计算前两个数之和得到的。
示例: 0, 1, 1, 2, 3, 5, 8, 13, 21, ………..
由于除前两项之外的每一项都是通过添加前两项获得的,因此我们可以生成一个规则来找到序列中的第 n 项。
Xn = X(n-1) + X(n-2) ,其中
X(n-1) 和 X(n-2) 是第 n 项的前两项。
例如:考虑斐波那契数列
n = 0 1 2 3 4 5 6 7 8 9
Xn = 0 1 1 2 3 5 8 13 21
第 9 项的计算方法如下
X9 = X(9-1) + X(9-2)
= X8+ X7
= 21 + 13
= 34.
以 main 函数开始程序。声明一个整型变量 n 来保存输入的项数。将前两项 X1 和 X2 设置为 0 和 1。 X1 = 0 和 X2 = 1。以及另一个整型变量 nextterm = 0。要求用户输入项数。将输入的值复制到 n。打印第一项 X1 和第二项 X2。然后通过添加 X1 和 X2 打印 nextterm。之后分配 X1 = X2; X2 = nextterm; 这个过程将继续,直到项数达到 n。
步骤 1: 调用头文件 iostream。
步骤 2: 使用命名空间 std。
步骤 3: 打开整型 main 函数;int main()。
步骤 4: 声明整型变量 n, X1 = 0, X2 = 1, nextterm=0。
步骤 5: 打印消息“Enter the number of terms”,并 读取字符到变量 n。
步骤 6: 打印前两项 X1 和 X2。
步骤 7: 使用 for 循环生成斐波那契数列。
步骤 8: 通过添加前两项计算 nextterm ; nextterm = X1 +X2。
步骤 9: 打印数列的 nextterm 。
步骤 10: 更新项 X1 = X2 和 X2 = nextterm。
步骤 11: 该过程继续 直到项数达到 n。
步骤 12: 退出。
#include <iostream>
using namespace std;
int main() {
int n, X1 = 0, X2 = 1, nextterm = 0;
cout << "Enter the number of terms: ";
cin >> n;
cout << "Fibonacci Series: ";
// Prints the first two terms.
cout << X1 << ", ";
cout << X2 ;
for (int i = 1; i < n; ++i) {
nextterm = X1 +X2;
X1 = X2;
X2 = nextterm;
cout << ", " << nextterm ;
}
return 0;
}
Enter the number of terms: 6 Fibonacci Series: 0, 1, 1, 2, 3, 5,