
在本关于递归的教程中,您将掌握函数中一种称为递归的独特过程的所有知识。此外,您还将看到一些适合通过递归解决的问题,例如数字阶乘、斐波那契数列等。
递归通常指函数通过自身调用来处理更小问题的重复调用过程。如果一个函数调用自身,则称该函数为递归函数,此类函数调用称为递归调用。精确地说,递归调用在达到基本情况时结束。
在 C 语言中,递归和迭代齐头并进,但它们各自处理特定的任务。例如,递归对于执行某些数学计算、排序、搜索、遍历等非常有用。但是,它并非适用于所有问题。所以我们可以说它不过是一种自定义函数。一些适合...
在 C 语言中使用递归是减少代码量的优雅方式。但事实是,理解其工作原理很困难。这是它的原型:
void recurse() // recursive function
{
........
recurse(); //recursive call
........
}
main() {
........
recurse(); // function call
........
}
为了更好地理解递归的工作原理,可以将其可视化如下。
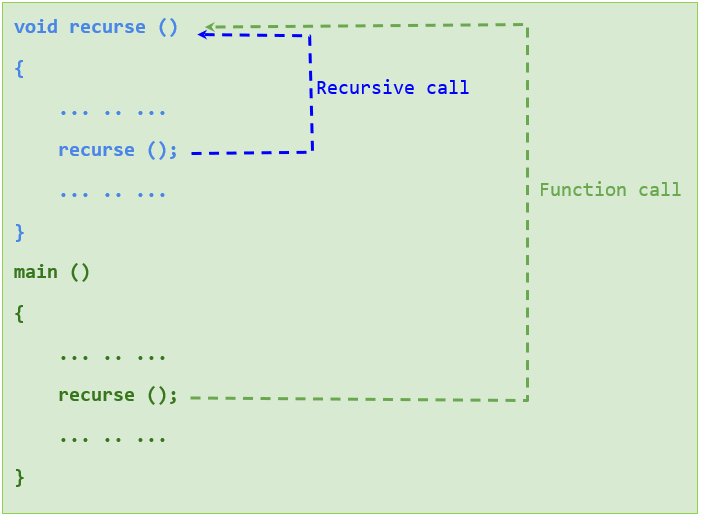
我们已经知道,在 C 语言中,执行从 main 函数开始,当它遇到函数调用时,控制权会转移到相应的函数。我们可以看到,函数的调用就像循环一样以周期性的方式进行。如我们所知,每个循环都必须有一个退出条件;否则,它将变成无限循环。递归函数也不例外。
在递归函数结构中,它有两个不可或缺的组成部分。它们是:
下面是一个简单的程序,它将通过递归函数计算到指定数字的所有数字的总和。
#include
int sum(int n);
int main()
{
int num, tot;
printf(" Calculate sum of the numbers upto:-> ");
scanf("%d", &num);
tot= sum(num);
printf("\n The result is %d", tot);
}
int sum(int n)
{
if (n !=0)
return (n + sum(n-1));
else
return n;
}
输出
Calculate sum of the numbers upto:-> 5 The result is 15
Calculate sum of the numbers upto:-> 10 The result is 55
此递归一直持续到变量 'no' 达到 '0'。发生这种情况时,编译器将退出程序。假设我们输入 5。main 函数将数字作为参数传递。然后数字减至 4,函数再次被调用。因此,执行 5+4+3+2+1 的加法,结果为 15。
让我们通过下图分解上述递归方法调用程序。

我们可以使用递归来确定任何数字的阶乘。在数学上,数字 n 的阶乘定义为:
n! = n x (n-1) x (n-2) ...... x 2 x 1
| 计算阶乘的通用方法 | 示例:5! |
|---|---|
| n! = n x (n-1)! | 5! = 5 x 4! |
| n! = n x (n-1) x (n-2)! | 5! = 5 x 4 x 3! |
| n! = n x (n-1) x (n-2) x (n-3)! | 5! = 5 x 4 x 3 x 2! |
| 5! = 5 x 4 x 3 x 2 x 1! | |
| n! = n x (n-1) x (n-2) x (n-3) ….3! | 5! = 5 x 4 x 3 x 2 x 1 => 120 |
| n! = n x (n-1) x (n-2) x (n-3) ….3 x 2! | |
| n! = n x (n-1) x (n-2) x (n-3) ….3 x 2 x 1! |
我们可以看到问题被分解为子问题,这些子问题使用相同的函数并重复调用,直到达到基本值。因此,每次调用时,整数都会与下一个较小的整数重复相乘,直到达到最低值 '1'。现在我们可以这样构建一个名为 'fact' 的递归函数:
#include
int fact( int n)
{
if(n <= 1)
return 1;
else
return n * fact(n - 1);
}
main()
{
int i;
printf (" Calculate factorial of --> ");
scanf("%d",&i);
printf("Factorial of %d is %d\n", i, fact(i));
}
Output:1 Calculate factorial of --> 5 Factorial of 5 is 120 Output:2 Calculate factorial of --> 10 Factorial of 10 is 3628800
假设我们输入 5。
下图将更清晰地展示在 C 语言中使用递归计算数字阶乘的方法。

斐波那契数列是一系列正整数,其中每个项是前两项的总和。该数列具有重要的数学意义。斐波那契数列以数字 0 和 1 开头,序列如下所示:
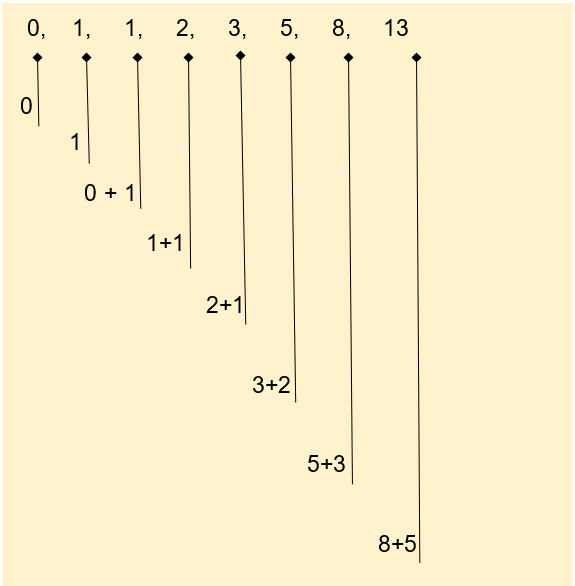
下面是一个使用迭代来执行斐波那契数列的示例程序。
#include
int main()
{
int i, n, c = 0, p = 1, t = 0;
printf( " How many terms do you want to show -> ");
scanf("%d", &n);
printf("Fibonacci Series: ");
for (i = 1; i <= n; ++i)
{
printf("%d, ", t);
t = c + p;
p = c;
c = t;
}
return 0;
}
在这个程序中,c 可以被视为当前值,p 可以被视为前一个值。我们已将 c 初始化为 1,将 p 初始化为 0。总和存储在变量 t 中,它被初始化为 0。这里使用 for 循环来防止迭代无限执行。在 for 循环的第一个周期:
它打印 t 的值 = 0,然后:
t = 0 + 1 = 1
p = 0
c = 1
在下一个周期:
打印 "1" (t 的值)
t = 1 + 1 = 2
p = 1
c = 2
... 依此类推。
现在,使用递归,我们可以用更少的代码做到这一点。我们所要做的就是定义一个名为 "fibn" 的函数,并在其中用适当的参数调用它。
int fibn (int i)
{
if(i == 0)
return 0;
if(i == 1)
return 1;
else
return fibn(i-1) + fibn(i-2);
}
main()
{
int i, n,a;
printf( " How many terms do you want to show -> ");
scanf("%d", &a);
printf("Fibonacci Series: ");
for (i = 0; i < a; i++)
printf("%d, ", fibn(i));
}
此程序将产生与之前完全相同的结果。fibn(i) 将被用户指定的次数调用,并递归调用该函数以产生精确结果,直到达到结束。
