Python 集合

在本教程中，您将掌握 Python 集合的所有知识；如何编写集合，Python 中的集合如何工作，如何对集合执行标准运算，如并集、交集和差集。除此之外，我们还将学习操作集合的方法。

数学上，集合可以定义为无序的、不同的对象的集合。同样，在 Python 中，集合是无序的唯一元素集合。需要明确的是，集合中的元素在内存中不是按照它们在集合中出现的顺序存储的。集合中的所有元素都必须是不可变的。但是集合本身是可变的，因此我们可以通过添加或删除元素来修改集合。

另一种变体称为冻结集合，顾名思义，它是静态的且不可变的。

Python 集合的关键特性

• 集合中的元素是唯一的，这意味着不允许重复元素。
• 集合是无序的，这意味着元素不遵循任何顺序。
• 集合不支持索引。
• 集合是可变的，而集合中的元素是不可变的

如何在 Python 中编写集合

可以使用两种方式定义集合：一种是通过花括号括起来的逗号分隔的元素，另一种是使用 set() 函数。

对于集合而言，不可变性比其他数据类型更重要，因为集合是可变的，而集合中的元素是不可变的。这意味着一旦创建，我们就无法更改元素。更确切地说，像整数、浮点数、字符串、元组等不可变数据类型可以作为集合的元素，但不应是列表、集合或字典，因为它们是可变的（可更改的）。集合可以包含任意数量的元素。

空集合： 通常使用不带参数的 set() 函数来定义空集合，以避免在使用空花括号 {} 时产生的歧义。Python 将空花括号 {} 视为字典，这是 Python 中的另一种数据类型，您将在下一个教程中学习。

emp_set=set()
print(type(emp_set))

emp_set={}
print(type(emp_set))

输出

<class 'set'>
<class 'dict'>

同质集合： 包含相同不可变数据类型元素的集合。

int_set = {1,2,3,4}
print("Homogenous set with integer elements:",int_set)
str_set = {'red','blue','green'}
print("Homogenous set with string elements:",str_set)

输出

Homogenous set with integer elements: {1, 2, 3, 4}
Homogenous set with string elements: {'green', 'blue', 'red'}

混合集合： 包含不同不可变数据类型元素的集合

mix_set={3.14,'prime',(1,2,3,5,7)}
print("Mixed set is ",mix_set)

输出

Mixed set is {3.14, 'prime', (1, 2, 3, 5, 7)}

Python 中的集合是如何工作的？

在 Python 中，集合通常用于验证元素的成员资格以及从序列中消除重复项。我们已经了解到 Python 集合不处理重复元素和可变元素。如果集合中存在任何重复元素，它将自动从序列中删除重复项；同样，如果集合中包含任何可变元素，Python 将引发 TypeError，如下所示：

S={1,2,3,1,2,3} # duplicate elements are automatically eliminated 
print (S)

输出

{1, 2, 3} 

S={ 'odd',[1,3,5]}
print(S)

输出

TypeError: unhashable type: 'list'

从上面的例子中，我们可以理解列表是不可哈希的。那么可哈希是什么意思？可哈希意味着可以进行哈希，进而表明对象或数据类型是固定的，一旦创建就无法更改。一个元素是可哈希的，当且仅当该元素是不可变的。例如，字符串和元组是不可变的，因此是可哈希的。相比之下，Python 列表是可变的元素，是不可哈希的。

如何访问集合

我们现在熟悉集合是唯一元素的无序集合。集合成员的存储方式与它们在集合中显示的方式不同。为了理解这一点，让我们检查下面的示例。

A=set('Green')
print(A)

输出

{'e', 'G', 'n', 'r'}

此外，我们可以发现它从集合(‘Green’)中消除了重复值 ‘e’，并返回了一个包含四个唯一元素的集合：

{'e', 'G', 'n', 'r'}.

由此，我们可以推断，无法像处理字符串和元组等其他数据类型那样，通过索引和切片来访问列表中的元素。

如何修改 Python 集合

集合的可变性使其可以通过添加单个或成组的元素来修改集合。添加到列表的两个常用方法是：

1. add()：用于向集合添加单个元素。

   如何向集合添加元素

   str_set = {'red','blue','green'}
   str_set.add("Black")
   print("New set after addition :",str_set) 
   

   输出

   New set after addition : {'blue', 'green', 'red', 'Black'}
   

2. update()：用于向集合添加多个元素

   如何向集合添加多个元素

   str_set = {'royal blue'}
   str_set.update((65,105,225))
   print("New set after addition :",str_set) 
   

   输出

   New set after addition : {65, 'royal blue', 225, 105}
   

如何从集合中删除元素

要从集合中删除元素，Python 集合提供了两种方法：discard() 和 remove()。区分 discard() 和 remove() 的唯一行为是，如果元素不在集合中，discard() 会保持集合不变，而 remove() 会引发 KeyError。这可以在下面的示例中说明。

A= {1,2,3,4,6,8}
A.discard(3)
print(A)
A.remove(4)
print(A)

A.discard(5)
print(A)
A.remove()
print(A) 

输出

{1, 2, 4, 6, 8}
{1, 2, 6, 8}
{1, 2, 6, 8}
KeyError: 3

要删除集合中的所有元素，我们可以使用 clear() 方法。我们也可以使用 pop() 方法删除集合中的最后一个元素。由于集合是无序的，我们无法预测 pop() 后的结果。要删除整个集合，我们可以使用 del 关键字。

A= {1,2,3,4,6,8}
A.pop()
print("Set after using pop method is",A)
A.clear()
print(A)
del A 

输出

Set after using pop method is {2, 3, 4, 6, 8}
set()

Python 集合运算和操作数

集合除了用于消除重复项和验证成员资格等用途外，还可以用于数学计算。四个常见的集合运算是并集、交集、差集和对称差集。我们可以通过使用方法在 Python 中执行这些运算。

如何在 Python 中添加/合并两个集合？

在 Python 中添加两个集合意味着将两个不同的集合合并为一个集合。可以使用称为并集的集合运算来连接两个集合。顾名思义，并集将两个不同的集合联合成一个新的集合。Python 中使用的并集操作符是 “|”。如果 A 和 B 是两个集合，那么 A & B 的并集表示为 A|B。

设我们的集合为

A 和 B 的并集将是一个包含 A 和 B 中所有唯一元素的新集合。重复的元素将从集合中排除。下面显示了 A|B 的维恩图。

集合的并集：A|B

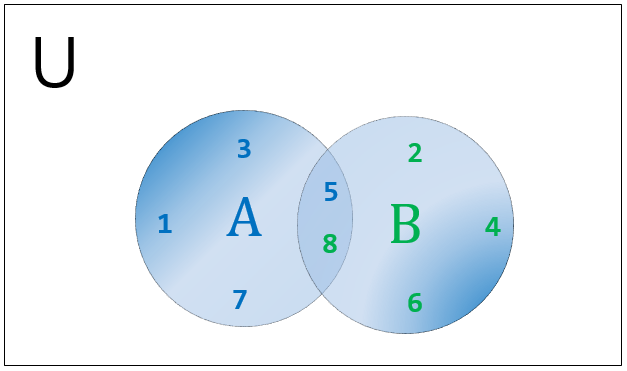
在 Python 中，集合的并集可以通过多种方式完成。它们列在下面：

• 使用集合操作符 (|) – 组合两个具有唯一元素的集合
• 使用 union() 方法 – 返回一个包含集合中所有元素的新集合。

A = {1,3,5,7,8}
B = {2,4,5,6,8}

print("A|B = ",A|B)
print("A.union(B) = ",A.union(B))
print("B.union(A) = ",B.union(A))
 

输出

A|B = {1, 2, 3, 4, 5, 6, 7, 8}
A.union(B) =  {1, 2, 3, 4, 5, 6, 7, 8}
B.union(A) =  {1, 2, 3, 4, 5, 6, 7, 8}

Python 中集合的交集是什么？

在 Python 中，两个集合 A 和 B 的交集是由两个集合中的共同元素组成的集合。两个集合的交集可以表示为 A&B，其中 & 是交集操作符。

A 和 B 的交集返回一个包含 A 和 B 中共同元素的新集合。换句话说，我们可以说重复值被视为共同元素。下面展示了 A&B 的维恩图。

集合的交集：A&B

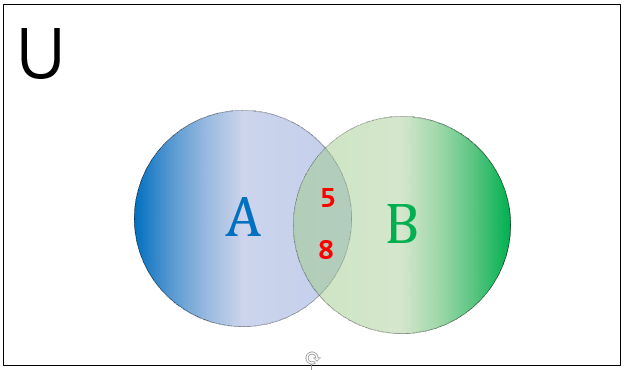
Python 可以通过使用交集操作符或 intersection() 方法来完成集合的交集。

A = {1,3,5,7,8}
B = {2,4,5,6,8}

print("A&B =",A&B)
print("A.intersection(B) = ",A.intersection(B))
print("B.intersection(A) = ",B.intersection(A))
 

输出

A&B = {8, 5}
A.intersection(B) =  {8, 5}
B.intersection(A) =  {8, 5}

如何在 Python 中找到集合的差集？

集合的差集比通常的数学差集是一个棘手的概念。然而，在两种情况下，我们都使用相同的操作符 (-) 来表示差集。为了无误地理解这个概念，假设 A 和 B 是两个具有不同元素的集合。集合 A 和 B 的差集可以用两种方式表示，但它们可能不相等。

• A-B：读作集合 B 从 A 中减去，得到集合 A 中存在但 B 中不存在的元素。
• B-A：读作集合 A 从 B 中减去，得到集合 B 中存在但 A 中不存在的元素。

下面图示了表示集合差集的维恩图。

集合差集：A-B

集合差集：B-A

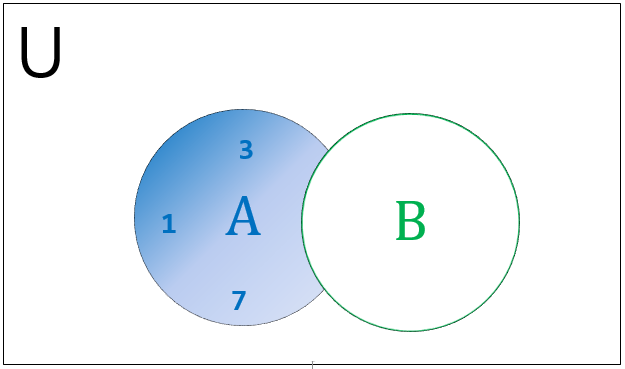
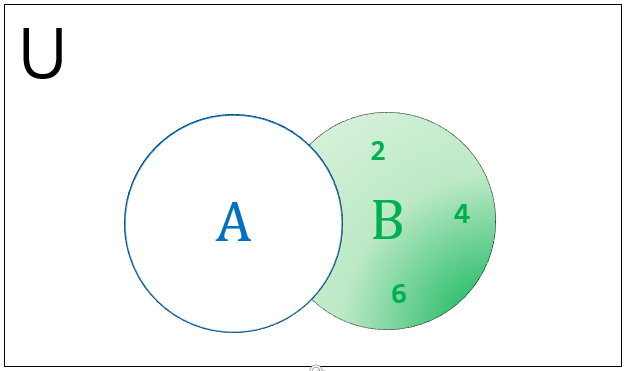
可以使用操作符或 difference() 方法在 Python 中执行集合差集，如下面的示例所示。

A = {1,3,5,7,8}
B = {2,4,5,6,8}

print("A-B = ",A-B)
print("B-A = ",B-A)

print("A.difference(B) = ",A.difference(B))
print("B.difference(A) = ",B.difference(A)) 

输出

A-B =  {1, 3, 7}
B-A =  {2, 4, 6}
A.difference(B) =  {1, 3, 7}
B.difference(A) =  {2, 4, 6}

Python 中的对称差集是什么？

Python 中的对称差集是一种集合运算，用于查找两个集合的对称差集。设 A 和 B 为两个集合，它们的对称差集是包含 A 和 B 中存在但不同时存在于两者中的元素的集合。换句话说，它是 A-B 和 B-A 的并集，即：

A^B =(A-B) |(B-A)

集合 A 和 B 的对称差集可以表示为 A^B，其中 ^ 是操作符。使用的方法是 symmetric_difference()。

对称差集可以用维恩图最好地说明

集合 A^B 的对称差集

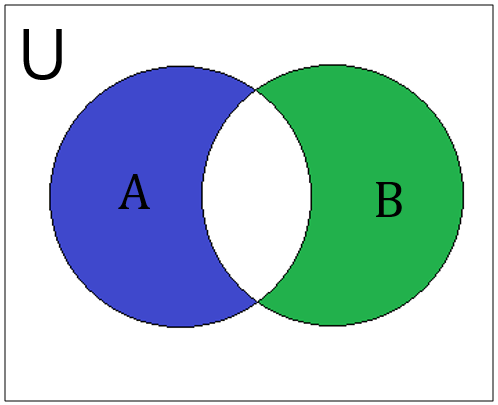
以下示例展示了对称差集的工作原理。

A = {1,3,5,7,8}
B = {2,4,5,6,8}

print("A^B = ",A^B)
print("A.symmetric_difference(B) = ",A.symmetric_difference(B))

 

输出

A^B =  {1, 2, 3, 4, 6, 7}
A.symmetric_difference(B) =  {1, 2, 3, 4, 6, 7}

Python 集合用于验证成员资格

集合的另一个重要运算是成员资格验证。这意味着我们可以使用成员资格运算符轻松检查子集或元素的出现。Python 中有两个成员资格运算符：

• in：仅当子集或元素存在于集合中时返回 true。
• not in：仅当子集或元素不在集合中时返回 true。

A = {1,3,5,7,8}

print(3 in A)
print(8 not in A)
 

输出

True
False

Python 内置函数

Python 集合具有一些内置函数来完成各种任务。以下是带有集合的内置函数列表。

集合中的方法

Python 集合有许多方法可以执行一些特定任务。其中一些我们在上一节中已经熟悉了。您可以参考下表来熟悉集合中使用的方法。

冻结集合

集合的另一种变体是冻结集合，正如其名称所示，它是所有元素都被冻结的集合。与集合不同，冻结集合中的所有元素在整个生命周期中都是固定的且不可变的（不可更改的）。因此，冻结集合是可哈希的，这意味着在创建后无法更改其元素。冻结集合的哈希值可以用作 字典 的键或作为另一个集合的集合元素。

如何创建冻结集合

使用 frozenset() 函数创建冻结集合。参数可以是集合或任何可变对象。如果参数为空，则 frozenset 函数将返回一个空冻结集合。以下示例让您了解如何创建冻结集合。

Fset=frozenset(['prime',1,2,3,5,7])
print(Fset)
Emp_Fset=frozenset()
print(Emp_Fset)
 

输出

frozenset({1, 2, 3, 5, 7, 'prime'})
frozenset()

冻结集合执行几乎所有在集合中有效的方法，如 copy()、difference()、intersection()、symmetric_difference()、union()、issubset()、issuperset() 和 isdisjoint()。由于冻结集合是不可变的，因此添加或删除元素的方法不适用，如果尝试修改冻结集合，结果将是 TypeError。