


一个数的阶乘是从1到该数所有整数的乘积。它只对正整数定义。对于给定的数n,阶乘有一个定义公式:
n! = n x (n-1) x (n-2) x ... x 2 x 1
例如,5的阶乘表示为5!,可以计算如下:
5 x 4 x 3 x 2 x 1 = 120
注意:零的阶乘值为1,即,0!= 1
下面给出了一个带有5!示例的详细图示。希望这能帮助您轻松理解递归函数的概念。
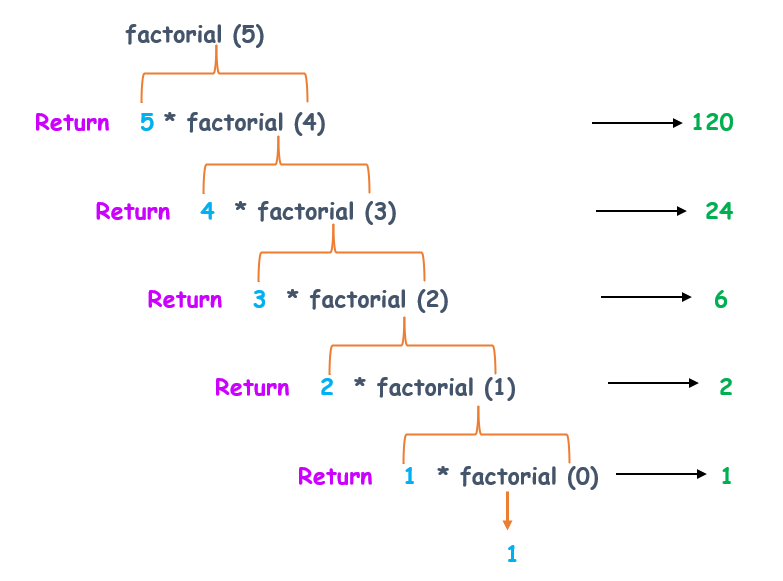
在这个R程序中,定义了一个函数**recur_fact()**来计算阶乘。在主函数中,我们直接将数字传递给**recur_fact()**来调用递归函数。
例如,我们调用函数**fact(5)**来查找5的值!该函数返回一个值,如**5 x fact(5-1)**,即在阶乘函数内部,它再次调用相同的函数,传入下一个数字4。这将一直持续到**fact(0)**返回1。最终,每个返回值的乘积将得到答案120。
在函数中,检查给定的数字是否小于或等于**1**,如果是,则`返回`值1,因为0!和1!本身的值都是1。如果条件不为真,则再次调用**recur_fact()**函数(即递归地),参数为**num-1**,并将`返回`值与**num**相乘,以计算到该数字为止所有整数的乘积。
步骤1:调用函数**recur_fact()**
步骤2:将数字作为**num**传递给函数。
步骤3:检查数字是否>**1**,如果是,执行步骤4,否则执行步骤5
步骤4:`返回`**num**乘以**(num - 1)**的阶乘的值
步骤5:`返回`**1**,即**num**达到<= 1
请参阅我们R程序集合中没有递归的简单阶乘程序。
recur_fact <- function(num) {
if(num <= 1) {
return(1)
} else {
return(num * recur_fact(num-1))
}
}
print(paste("The factorial of 5 is",recur_fact (5)))
[1] "The factorial of 5 is 120"