


设想这样一种情况:我们正在规划自己的下一步行动,但有人正在对抗我们,因此我们的计划会受到对手活动的影响。应用于这种情况的方法称为对抗搜索。在AI领域,搜索一词指的是博弈。
在我们之前的专题中,我们讨论了与单个智能体相关的搜索策略。但有些情况下,多个智能体在一个环境中工作。这种情况主要发生在博弈中。
一个拥有多个智能体的环境称为多智能体环境(您可以点击我们的第五个专题任务环境,了解有关多智能体环境的更多详细信息)。在这里,每个智能体将作为彼此的对手,相互对抗。每个智能体都必须考虑其他智能体的行动以及这些行动对其性能的影响。
因此,对抗搜索可以定义为一种博弈技术,其中智能体的环境具有竞争性特征。智能体试图探索单一搜索空间以找到解决方案。对抗搜索通常可以称为博弈。
示例:国际象棋、交易、战争。
我们改变了我们的状态,但我们无法控制下一个状态。对手将以一种不可预测且与我们对抗的方式改变下一个状态。
从数学上讲,这种搜索方法基于“博弈论”的概念。根据博弈论,博弈在两个或更多玩家之间进行,其中一个必须赢得博弈,而其他人则自动输掉博弈以完成博弈。
这种搜索方法是人工智能领域最重要的之一。它将为复杂情况下的多玩家环境提供解决方案。
它将为以下情况提供解决方案:
对抗搜索已应用于许多领域,下面列出了一些应用。
我们已经讨论了一些搜索方法。对于这种正常搜索,需要遵循一系列操作才能达到目标或结束游戏。但对于对抗搜索,结果将取决于玩家,他们将改变结果或决定游戏结果。由于玩家将尝试在有限时间内以最短路径赢得游戏,因此解决方案将是最佳解决方案。
以下是对抗搜索的类型:
在人工智能中,Minimax 是一种用于博弈论的决策策略,旨在最小化失败几率并最大化获胜几率。它也称为鞍点。它基于两个玩家,如果一个玩家赢得游戏,另一个玩家将自动输掉游戏。它可以说是一种回溯算法。我们在日常生活中玩的游戏,如井字棋、西洋双陆棋、Mancala、国际象棋等,都模拟了这种策略。
在 Minimax 策略中,两个玩家分别被称为最小化器和最大化器,其中最大化器试图获得尽可能高的分数,而最小化器则试图执行相反的操作,获得尽可能低的分数。它遵循 DFS 概念。这里的游戏在最大化器和最小化器之间交替进行。当最大化器完成移动后,下一步轮到最小化器。最大化器所做的移动是固定的,不能更改。这个概念被用于 DFS 策略;路径不能在中间更改。
示例

在上面的例子中,两个玩家是 MIN 和 MAX。MAXZ 通过选择一条路径并探索该路径的所有节点来开始游戏。MAX 然后将回溯到初始节点并选择提供最大效用值的最佳路径。之后,轮到 MIN。它也会探索一条路径并回溯。在这里,MIN 将选择一条路径,该路径可以最小化 MAX 的获胜机会或效用值。
| 优点 | 缺点 |
|---|---|
|
|
Alpha-beta 剪枝可以看作是 Minimax 算法的一种高级形式。Minimax 策略的主要缺点是时间消耗大,因为它会深入探索每个节点以提供最佳路径。Alpha-beta 剪枝将大大减少这个问题。这种方法使我们能够更快甚至更深入地搜索。它在 Minimax 函数中使用了两个额外的参数,称为 alpha 和 beta。它还通过探索减少的节点数量来缩短搜索。使用剪枝技术剪除不需要的分支。因此称为 alpha-beta 剪枝。在这里,Alpha 是最大化器在特定级别可以拥有的最佳可能值。而 Beta 是最小化器在特定级别可以拥有的最佳可能值。
示例
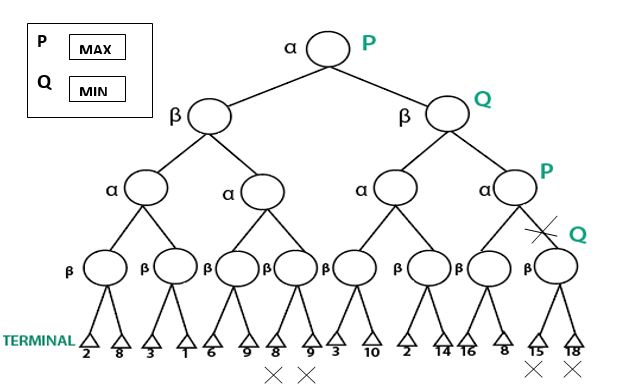
在上图中,P 和 Q 是两位玩家。设 P 是试图通过最大化获胜机会来赢得比赛的人,Q 是试图最小化 P 获胜机会的人。这里 alpha 代表节点的最大值,beta 代表节点的最小值。
| 优点 | 缺点 |
|---|---|
|
|