


现在您已经从我们之前的教程中了解了什么是非启发式算法。在人工智能中,搜索策略的另一个类别是**启发式搜索算法**。
顾名思义,启发式搜索算法**包含有关目标状态的信息**,这将使搜索更有效。它包含一系列关于目标状态与当前状态的接近程度、路径成本、如何达到目标等知识。启发式搜索算法在大型数据库中非常有用,在这些数据库中,非启发式搜索算法无法得出准确的结果。
启发式搜索算法也称为**启发式搜索**,因为它使用了启发式的概念。启发式函数是一个用于衡量当前状态与目标状态接近程度的函数,启发式属性用于找出在路径成本方面到达目标状态的最佳路径。
考虑一个在谷歌地图上搜索您想去的地方的例子。将当前位置和目的地地点提供给搜索算法,以计算准确的距离、所需时间和该特定路线上的实时交通更新。这是使用启发式搜索算法执行的。
启发式搜索算法可分为4种主要类型。

它是一种基于启发式值**h(n)**执行的简单搜索。它维护两个列表:**OPEN**用于新的未扩展节点,**CLOSE**用于已扩展节点。每次迭代都会扩展启发式值最小的节点。然后,其所有子节点都被扩展并添加到封闭列表。然后将启发式函数应用于封闭列表,并保存最短路径的节点,其余节点则被丢弃。该算法从开放列表上的初始状态节点开始。在每个循环中,开放列表中h(n)值最小的节点被扩展,并生成其子节点并保存在封闭列表中。然后将启发式函数应用于子节点,并根据其启发式值将其放置在开放列表中。
该过程一直持续到选择目标状态进行扩展。
在给定启发式函数的纯启发式搜索中,使用的最简单方法是
f(n) = h(n)
其中f(n)是成本函数,h(n)是启发式函数。对于PHS算法,即使存在目标节点,也不能保证在无限图中终止。
示例
这里返回的解决方案长度为4,即使存在长度为3的解决方案。PHS在扩展节点时,或从节点n到达目标节点的成本时,只考虑h(n),即启发式函数或到目标的估计成本。它不考虑从起始状态g(n)到达节点n的成本。
| 优点 | 缺点 |
|---|---|
|
|
顾名思义,它总是选择当时看起来最好的路径。它是广度优先搜索和深度优先搜索算法的结合,并利用了这两种算法的优点。它还使用启发式函数执行搜索过程。它有助于在每一步选择最乐观的节点。最接近目标节点的节点被扩展,并且最接近的成本通过启发式函数进行近似。
让我们以旅行推销员问题为例进行讨论。
推销员收到一份要访问的城市地点列表。他必须找到最佳路线,以便尽可能减少旅行时间。在这里,他可以从他当前的位置选择2个或更多地方去。他必须选择距离最短的地方。
例如,
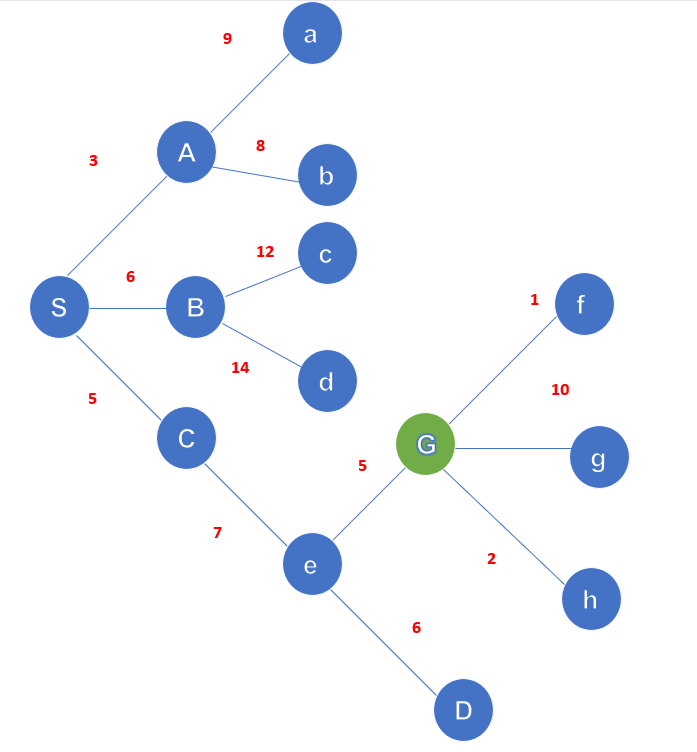
节点成本存储在优先级队列pq中。
程序可以是这样的
我们的源节点或起始节点是S,目标节点是G。pq最初是S。我们从pa中移除S并添加子节点**{A, C, B}**(C放在B之前,因为C的成本较低)。
现在A被移除,a,b被添加到pq **{C, B, a, b}**。移除C并添加e到pq **{B, e, a, b}** B被移除,c,d被添加到pq **{ e, a, b, c, d}** 。现在e被移除,因为我们的目标已经达到。
| 优点 | 缺点 |
|---|---|
|
|
它结合了贪婪搜索和统一成本搜索(在之前的专题中讨论过)的优点。A*搜索的启发式值计算为贪婪搜索和统一成本搜索中启发式成本的总和。
f(x) = h(x) + g(x)
选择f(x)最短的节点。
示例

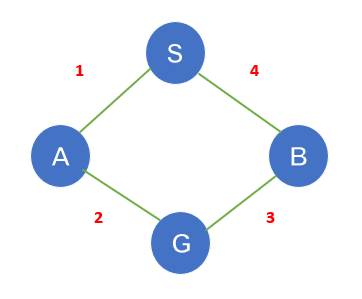
这里S是初始节点,G是目标节点。边上(绿色)的数字是节点之间的距离,节点上(红色)的数字是启发式值。过程从节点S开始。S的g(x)=0,S的h(x)=5。因此,S的f(x)=0+5=5。
现在从S,我们可以去A或G。计算每个节点的f(x)。
S到A = 1 + 3 = 4
S到G = 0 + 10 = 10。
由于S到A的成本较低,我们继续走这条路径。
A到B = 2 + 4 = 6
A到C = 1 + 2 = 3
这里A到C的成本较低,继续走这条路径。
C到D = 3 + 6 = 9
C到G = 4 + 0 = 4
目标已达到
我们得出结论,S---A---C---G是从S到G最具成本效益的路径。
| 优点 | 缺点 |
|---|---|
|
|
考虑到树搜索的情况,我们不保留此列表,并且会多次访问同一节点。因此,A*树会因这种多次探索而浪费时间。通过添加不重复扩展节点的规则,可以消除或处理此限制或缺点,即使用A*图搜索或简单地称为图搜索。
在图搜索中,我们保留一个已探索集合的列表,以跟踪已扩展的节点,以便它们不会再次被访问。图搜索只有当两个节点(例如A和B)之间的前向成本h(A)-h(B)小于或等于这些节点之间的后向成本g(A)-g(B)时才被认为是最佳的。图搜索技术的这一特性称为**一致性**。
示例

解决方案与树方法非常相似;唯一的区别是维护了一个已探索节点的跟踪,以便它们永远不会被重新探索。
初始节点是S,路径将是
从S到D
F = 2(S-D) + 5(D) = 7
F = 2 + 5 = 7
D到B ----- f = 2(S-D) + 1(D-B) + 4(B) = 7
F = 2 + 1 + 4 = 7
B到E -------- f = 3(S-D+D-B) + 1(B – E) + 3 (E) = 7
F = 3 + 1 + 3 = 7
E到G -------- f = 4 (S-D = D-B + B-E) + 3(E-G) + 0(G) = 7
F = 4 + 3 = 7。
S----D---B---C---E---G
| 优点 | 缺点 |
|---|---|
|
|