


在我们之前的主题中,我们讨论了AI的问题解决任务。算法是解决问题的主要技术之一。AI中有许多类型的算法。其中,我们可以在这里讨论一些主要类别。
算法可以定义为编程过程的起点,而**AI算法可以定义为机器学习的一个扩展子集,它指导计算机学习如何自行操作**。人工智能算法已被用于解决数百万个问题,因此很难列出每一个算法。所以,让我们来讨论人工智能算法的三个主要类别。
将数据分类到不同类别的技术称为分类。分类问题的主要目标是确定问题属于哪个类别。在AI中,称为分类算法的算法用于识别给定数据集的类别,这些类型的算法用于预测决策性数据的输出。分类算法是一种监督学习技术,程序从观察中学习,然后将新的观察分类到几个组中。分类过程有助于将大量数据分离为不同的值,如0/1、真/假。这些算法主要用于预测分类数据的输出。可以使用此方法找到模式的相似性,如相似的单词、数字序列等。
最广泛使用的分类算法
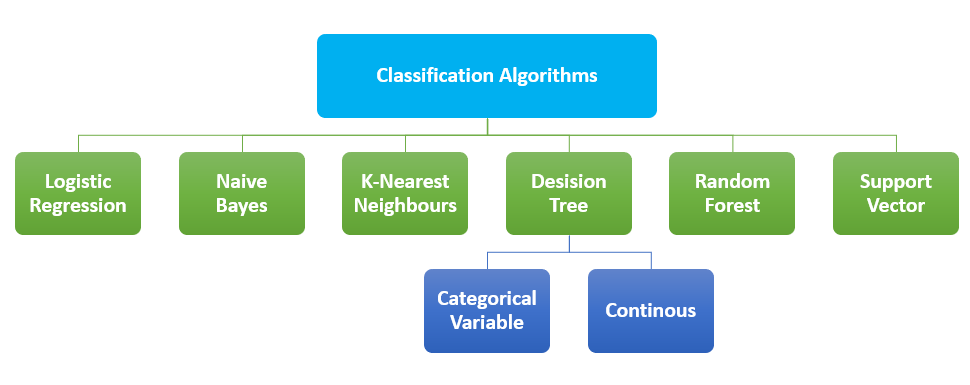
尽管听起来像是回归,但它用于对样本进行分类,属于分类算法。该模型使用了预测建模作为回归的概念。在逻辑回归中,使用一组自变量来预测分类因变量。该算法的结果是介于0和1之间的概率值。它可以使用离散数据集对新数据进行分类。它之所以重要,是因为它提供了概率。
该算法基于贝叶斯定理。它是最简单但功能强大的解决方案。该算法可用于基于历史结果的二元分类和多类分类。该算法的准确性取决于强假设。贝叶斯定理可用于确定一个事件的发生对另一个事件概率的影响。
它是最简单的分类算法之一。KNN只是存储训练数据的出现情况,而不是构建一个通用的内部模型。分类是基于每个点的K个最近邻的多数投票。在计算给定查询与数据中所有可用示例之间的距离之后,选择有限数量的最接近给定查询的示例。这个数字在KNN算法中用字母K表示。然后投票选出最频繁的标签。这是对KNN工作原理的简单描述。这可以归类为分类和回归。
决策树方法可以说是可视化决策过程最直观的方式。一个决策将产生一系列规则,可用于对给定数据进行分类。它以树状结构构建分类模型。给定的数据集被划分为越来越小的子集。最终结果将是一个带有决策节点和叶节点的树状结构。该方法从树的根开始预测给定输入的类别。根据目标变量的性质,有两种类型的决策树
决策树的主要问题之一是它可能导致过拟合
它在数据集的各种子样本上使用多个决策树。为了对抗过拟合和提高预测准确性,该方法将平均结果作为模型的预测。凭借结果的准确性,它可以用来解决复杂问题。该方法的实现有些困难,并且需要更多时间来形成预测。
为了对数据点进行分类,支持向量机在N维空间中使用一个超平面。这里的特征数量用N表示。N可以是任何数字,但数字越大,实现模型就越困难。如果N=2,我们可以将超平面看作是一条分隔标签的线。这条线可以被认为是决策边界。落在超平面不同侧的任何东西都被分配到不同的类别。
| 算法 | 优点 | 缺点 |
|---|---|---|
| 逻辑回归 |
|
|
| 朴素贝叶斯 |
|
|
| K-最近邻 |
|
|
| 决策树 |
|
|
| 随机森林 |
|
|
| 支持向量机 |
|
|
将数据点分成几组的过程称为聚类。每个组中的数据点彼此相似,而与其他组中的数据点不相似。相似的项目被分组。最常见的聚类算法是
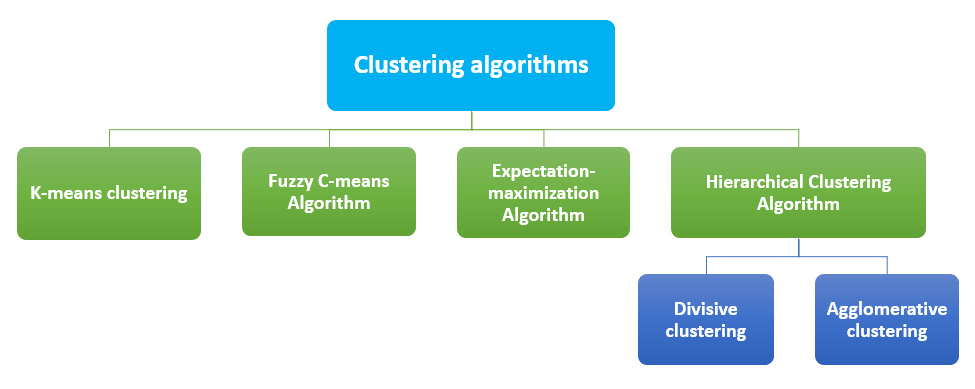
这是最简单的学习方法。在AI中,K-均值将数据分组到簇中以研究其相似性。数据点被分成K个簇。为每个簇计算一个质心,然后评估簇的质心与数据点之间的距离。
概率是FCM的基本工作原理。这种方法之所以被称为模糊,是因为它不为任何数据点分配任何特定簇的绝对成员资格。每个数据点都被分配一个属于任何簇的概率值。
高斯分布是该方法的工作原理。为缺失的数据点选择随机值,并用这些猜测估计第二组数据。这些新值可用于为第一组创建更好的猜测,并且该过程将继续,直到算法达到一个固定点。
在该模型中,相似的对象被分组到簇中。最终结果是一组簇,其中每个簇与其他簇不同,并且每个簇内的对象彼此大致相似。层次聚类算法有两种类型
| 算法 | 优点 | 缺点 |
|---|---|---|
| K-均值算法 |
|
|
| 模糊C-均值算法 |
|
|
| 期望最大化算法 |
|
|
| 层次聚类算法 |
|
|
回归算法主要用于预测。AI中的回归可以定义为找出变量之间关系的数学方法。回归模型的输出是数值。常见的回归算法有
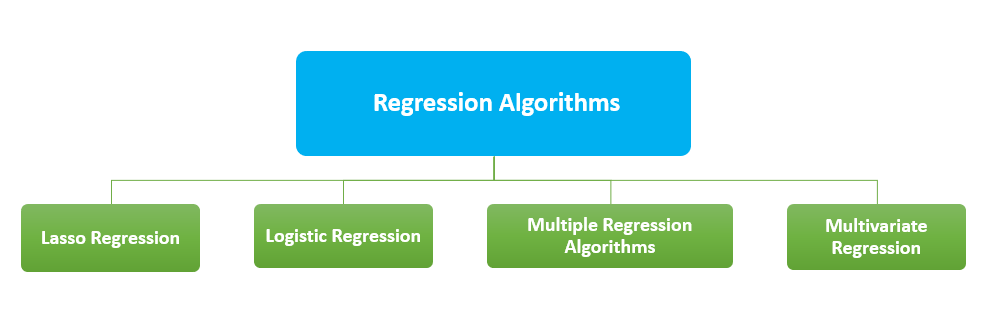
Lasso回归是一种使用收缩的方法。LASSO代表“最小绝对收缩和选择算子”。通过对数据点施加限制并将其中一些收缩为零值,该算法获得预测变量的子集。该子集能够最小化响应变量的预测误差。
该方法主要用于二元分类。分析一组变量并预测一个分类结果。
它以多个解释变量作为输入。它可以被描述为线性回归和非线性回归算法的组合。可以使用多元回归来评估因变量和多个预测变量之间的关系。
该算法使用多个预测变量进行操作。它是多元回归的扩展。该算法主要应用于零售行业的产品推荐引擎。
| 算法 | 优点 | 缺点 |
|---|---|---|
| Lasso回归 | 模型更简单,更易于解释 | 不适用于分组选择 |
| 逻辑回归 | 更易于实现。不易过拟合 | 无法解决非线性问题。难以捕捉复杂关系。 |
| 多元回归 | 比简单回归更准确。能够识别异常。 | 使用不完整的数据,并错误地得出相关性即因果关系的结论。 |
| 多变量回归 | 帮助我们理解数据集中变量之间的关系。 | 不适用于较小的数据集。 |
算法在实现、准确性、性能和处理时间方面各有优缺点。以上只是一些算法及其简要介绍。如果您想了解更多相关信息,请访问我们的机器学习教程。