


在人工智能中,解决问题的通用技术是搜索。对于一个给定的问题,需要考虑所有可能的方法,从初始状态达到现有目标状态。人工智能中的搜索可以定义为寻找给定问题解决方案的过程。搜索策略用于指定选择哪条路径才能达到解决方案。
搜索算法有四个基本属性用于比较效率。
搜索算法主要根据搜索问题分为两类;
无信息搜索算法不知道领域知识,例如接近度、目标位置。它只知道如何遍历以及如何区分叶节点和目标节点,因此它以暴力方式操作,因此也称为暴力算法。它在没有任何先验知识的情况下搜索每个节点,因此也称为盲目搜索算法。
无信息搜索算法可分为六种主要类型

它是遍历树或图最常见的搜索策略。它使用广度优先搜索过程,因此称为广度优先搜索。该过程从树的根节点开始,在进入下一层节点之前扩展到第一层的所有后继节点。使用基于先进先出 (FIFO) 概念的队列数据结构来实现此方法。由于它返回一个解决方案(如果存在),因此可以称之为完备算法。
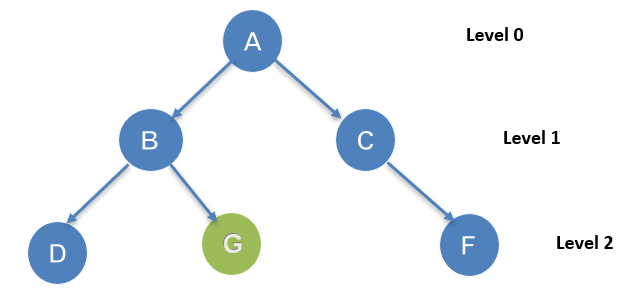
搜索过程从根节点 A 开始。这里的目标节点是 G。从节点 A 开始,它将按照 A-B-C-D-G 的顺序遍历。它将按层遍历。
| 优点 | 缺点 |
|---|---|
|
|
它是一个类似于 BFS 的过程。搜索过程从根节点开始,沿着每条路径走到最大深度,然后回溯,再进入下一条路径。使用基于后进先出 (LIFO) 概念的栈数据结构来实现该过程。
示例:
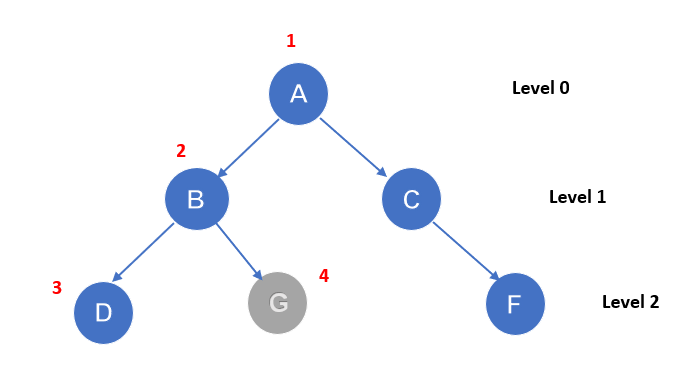
搜索过程从根节点 A 开始。这里的目标节点是 G。从节点 A 开始,它将按照 A-B-D-G 的顺序遍历。它将按深度遍历。
| 优点 | 缺点 |
|---|---|
|
|
它与深度优先搜索非常相似,但有一个预设的限制。DFS 的主要缺点是无限路径,这可以通过深度限制搜索来解决。在这里,达到限制的节点被视为没有进一步的后继节点。它可以被称为 DFS 的扩展和完善版本。
深度限制搜索将在两种条件下终止。
示例
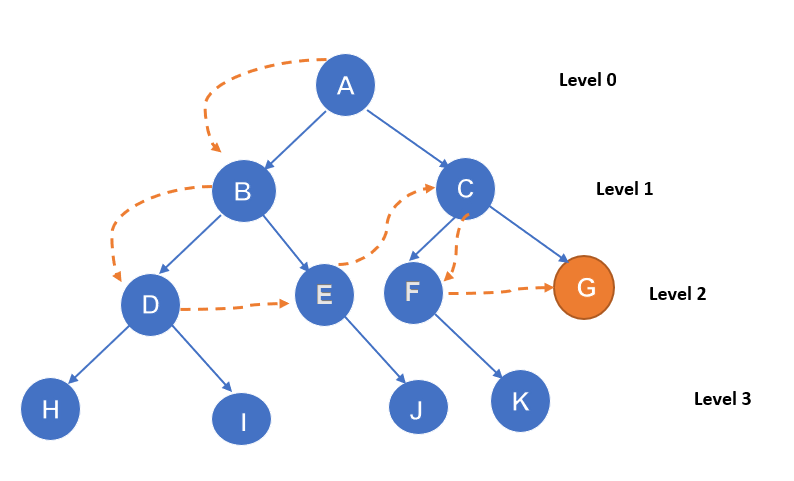
搜索从节点 A 开始。该过程的限制设置为 l=2。我们的目标状态是节点 G。过程是 A-B-D-E-C-F-G。
| 优点 | 缺点 |
|---|---|
|
|
它用于遍历加权树或图。它与 DFS 和 BFS 都不同。这里成本被视为一个因素。有不止一条路径可以达到目标。选择成本最低的路径。为了遍历路径,选择成本递增的顺序。如果每次转换的成本相同,那么它就可以说类似于 BFS。
示例。
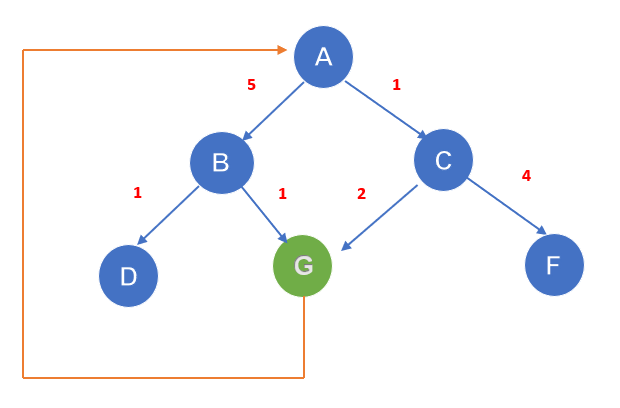
如果起始节点是 A,要达到的目标是 G,那么它将遍历 A-C-G。成本将是 3。
| 优点 | 缺点 |
|---|---|
|
|
它是 DFS 和 BFS 的结合。它将找到最佳深度限制,并且该限制会逐渐增加,直到找到目标。该算法执行到某个深度限制的深度优先搜索,并且该深度限制在每次迭代后都会增加,直到达到目标。BFS 的速度和 DFS 的内存效率在此迭代加深深度优先搜索中结合在一起。对于搜索空间大且目标节点深度未知的情况,这可能更有用。
示例

第一次迭代------A
第二次迭代------A,B,C
第三次迭代------A,B,D,E,C,F,G
第四次迭代------A,B,D,H,I,E,C,F,K,G
目标节点在第四次迭代中找到。
| 优点 | 缺点 |
|---|---|
|
|
它同时执行两次搜索。一次从起点开始,称为正向搜索;另一次从终点开始,称为反向搜索。一个单一的图被两个小的子图替换,一个从初始顶点开始,另一个从最终顶点开始。当这两个图相互交叉时,搜索过程停止。它可以使用 BFS、DFS、DLS 等搜索技术。
示例

算法在两个子图相遇的节点 I 处终止。
| 优点 | 缺点 |
|---|---|
|
|