


在本教程中,我们将借助示例学习 C++ 中的位运算符。
C++ 中的位运算符对整数数据进行单个位级别的操作。这些操作包括位测试、位设置和位移位。
例如
a & b;
a | b;
为了在 C++ 中对单个位执行操作,使用了位运算符。它们只兼容 char 和 int 数据类型。C++ 中主要有 6 种位运算符
| operator | 其描述 |
|---|---|
| & | 按位与 |
| | | 按位或 |
| ^ | 按位异或 |
| ~ | 按位一补码 |
| << | 按位左移 |
| >> | 按位右移 |
这些运算符是必需的,因为计算机 CPU 的算术逻辑单元 (ALU) 在位级别执行算术操作。
当且仅当两个操作数都为 1 时,按位与 & 运算符返回 1。否则,它将返回 0。
下表显示了按位与运算符的操作。设 a 和 b 是两个只接受二进制值(即 1 和 0)的操作数。
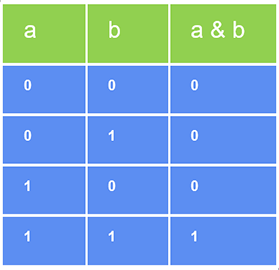
上面给出的表格被称为按位与运算符的“真值表”。
让我们检查两个整数 15 和 36 的按位与操作

#include <iostream>
using namespace std;
int main() {
// declare variables
int a = 15, b = 36;
cout << "a = " << a << endl;
cout << "b = " << b << endl;
cout << "a & b = " << (a & b) << endl;
return 0;
}
输出
a = 15 b = 36 a & b = 4
在前面的示例中,我们声明了两个变量 a 和 b。请注意这一行
cout << "a & b = " << (a & b) << endl;
我们在这里对变量 a 和 b 进行按位与操作。
如果至少有一个操作数为 1,则按位或 | 运算符返回 1。否则,它返回 0。
下表演示了按位或运算符。设 a 和 b 是两个只具有二进制值(1 或 0)的操作数。
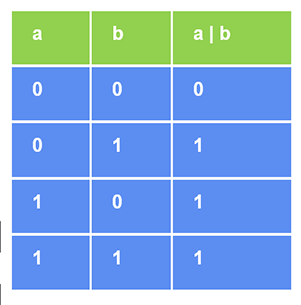
让我们检查两个整数 15 和 36 的按位或操作

#include <iostream>
int main() {
int a = 15, b = 36;
cout << "a = " << a << endl;
cout << "b = " << b << endl;
cout << "a | b = " << (a | b) << endl;
return 0;
}
输出
a = 15 b = 36 a | b = 47
当且仅当其中一个操作数为 1 时,按位异或 ^ 运算符返回 1。但是,如果两个操作数都为零或都为一,则结果为零。
下表演示了按位异或运算符。设 a 和 b 是两个只具有二进制值(1 或 0)的操作数。
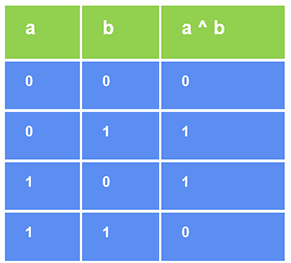
让我们检查两个整数 12 和 25 的按位异或操作

#include <iostream>
int main() {
int a = 12, b = 25;
cout << "a = " << a << endl;
cout << "b = " << b << endl;
cout << "a ^ b = " << (a ^ b) << endl;
return 0;
}
输出
a = 12 b = 25 a ^ b = 21
a = 12 和 b = 25 的按位异或结果是 21。
按位补码运算符是一种一元运算符(主要只作用于一个操作数)。它用 **~** 表示,它将二进制数字 1 转换为 0,将 0 转换为 1。
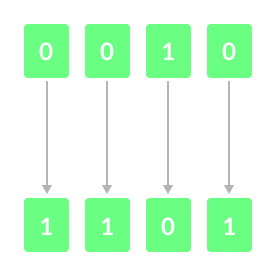
值得注意的是,任何整数 N 的按位补码等于 -(N + 1)。
让我们考虑一个整数 37。根据规则,37 的按位补码应该是 -(37 + 1) = -38。让我们检查我们是否得到了正确的答案。

在前面的示例中,**00100101** (37) 的按位补码是 **11011010**。当我们将这个结果转换为十进制时,我们将得到 218。
需要注意的是,我们不能简单地将结果转换为十进制并获得所需的输出。这是因为二进制结果 **11011010** 也等价于 -38。
要理解这一点,我们必须首先计算 -38 的二进制输出。为了计算负整数的二进制,我们使用 2 的补码。
例如:

在这种情况下,38 的 2 的补码(即 -38)是 11011010。在上一节中,我们计算了 37 的按位补码,该值与该数字等价。
因此,37 的按位补码是 -38。
#include <iostream>
int main() {
int num1 = 25;
int num2 = -160;
cout << "~(" << num1 << ") = " << (~num1) << endl;
cout << "~(" << num2 << ") = " << (~num2) << endl;
return 0;
}
输出
~(25) = -26 ~(-160) = 159
在前面的示例中,我们声明了两个整数变量 num1 和 num2,并分别用值 25 和 -160 初始化它们。
然后我们使用代码 **(~num1) 和 (~num2)** 分别计算并显示了它们的按位补码。
**25 = - (25 + 1) = -26** 的按位补码
即 **~35 = -36**
**-160 = - (-160 + 1) = - (-159) = 159** 的按位补码
即 **~(-160) = 159**
在 C++ 编程中,有两种移位运算符
右移运算符将所有位向右移动指定的位数。它用 >> 表示。
当我们向右移动一个数字时,我们丢弃最低有效位并用零替换它们。
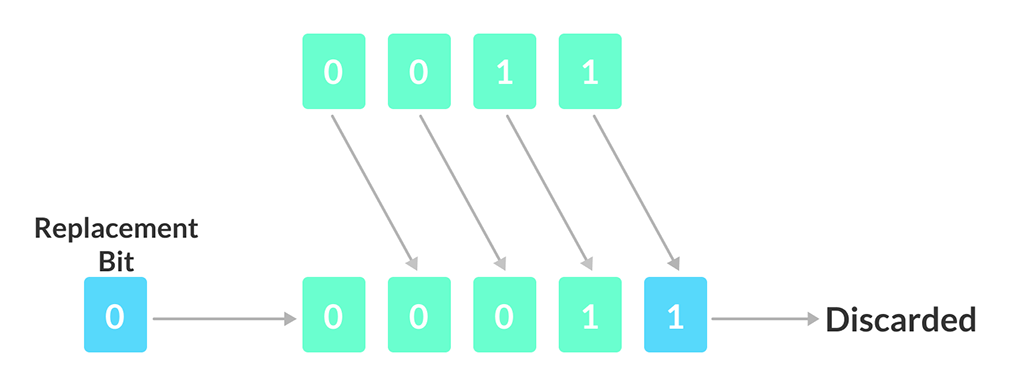
我们有一个 4 位数字,如上图所示。当我们对其执行一位右移操作时,每个单独的位都向右移动一位。结果,最右边的位被丢弃,留下最左边的位为空。这个空位已经被 0 填充。
左移运算符将所有位向左移动指定的位数。它由符号 << 表示。
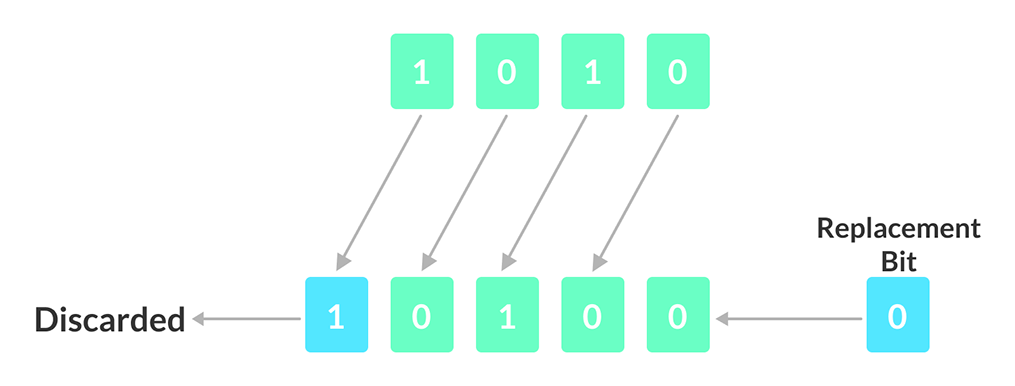
这里显示一位左移
我们有一个 4 位数字,如上图所示。当我们对其执行 1 位左移操作时,每个单独的位都向左移动一位。
结果,最左边的位被丢弃,而最右边的位留空。这个空位已经被 0 填充。
#include <iostream>
int main() {
// declaring two integer variables
int num = 212, i;
// Shift Right Operation
cout << "Shift Right:" << endl;
// Using for loop for shifting num right from 0 bit to 3 bits
for (i = 0; i < 4; i++) {
cout << "212 >> " << i << " = " << (212 >> i) << endl;
}
// Shift Left Operation
cout << "\nShift Left:" << endl;
// Using for loop for shifting num left from 0 bit to 3 bits
for (i = 0; i < 4; i++) {
cout << "212 << " << i << " = " << (212 << i) << endl;
}
return 0;
}
输出
Shift Right: 212 >> 0 = 212 212 >> 1 = 106 212 >> 2 = 53 212 >> 3 = 26 Shift Left: 212 << 0 = 212 212 << 1 = 424 212 << 2 = 848