C++ 递归

在本教程中，我们将探讨什么是递归及其工作原理。我们还将学习递归函数的特性，以及一些面试中经常问到的递归程序，如数字阶乘、斐波那契数列等，并附带其 C++ 代码。那么，让我们开始吧！

什么是递归？

递归函数是一种调用自身的函数。这种方法主要被称为递归。

递归是函数调用自身的子程序以解决复杂程序的过程。与需要大量精力和时间来解决相同问题的迭代方法不同，递归将程序分解为子任务并重复调用。因此，调用自身的函数称为递归函数，而函数调用自身的过程称为递归。递归最重要的方面是它有一个终止递归的基准情况。因为递归函数会无限地调用自身，程序总是可能进入无限循环。所以，如果我们使用 if...else 语句来创建终止基准情况，程序每次都会检查基准情况条件，避免进入无限循环。

递归的工作原理

与其他解决问题的方法相比，递归方法能够更成功地解决问题。递归过程将问题分解为函数子任务，并重复调用相同的函数以接近最终解决方案。这个过程将一直持续到我们找到问题的最终解决方案。每次发现解决方案的一部分时，它都会作为栈数据结构存储在内存中，然后弹出以获得最终解决方案。

为了在接近解决方案时退出递归过程，需要验证一个基本条件。这个基本条件通过条件语句检查，防止递归过程进入无限循环。如果基本条件因任何原因失败，程序将进入无限循环，我们将永远无法达到程序的解决方案。

以下语法展示了 C++ 中递归的工作方式。

void function_name() // recursive function
{
    ........
    function_name(); //recursive call 
    ........
}
main() {
    ........
    function_name(); // function call
    ........
}
 

下图展示了递归如何通过重复调用递归函数来工作。

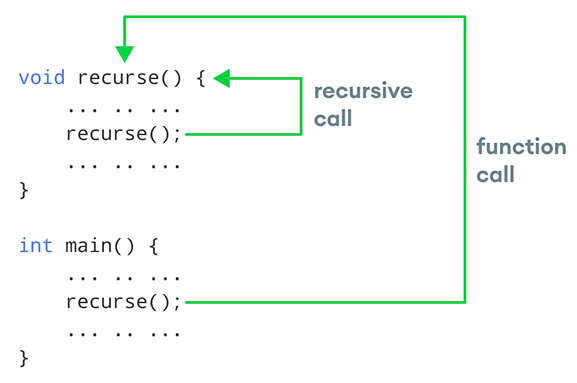
这里的 recursion() 是一个用户定义的函数。我们已经知道 C++ 的执行从 main 函数开始，当它遇到函数调用时，控制权将转移到相应的函数。我们可以看到函数调用以循环的方式执行，就像一个循环一样。正如我们所知，每个循环都必须有一个退出状态；否则它将变成无限循环。递归函数也不例外。

为了防止无限递归，可以使用决策语句（if、if.. else）。

C++ 中有两种类型的递归函数

• 直接递归：直接递归发生在函数调用自身时，如前面的程序所示。
• 间接递归：间接递归发生在函数调用另一个函数，然后该函数再调用原始调用函数时。

C++ 递归的优点

• 在递归程序中，使用的代码行数更少，使代码看起来更短、更简洁。
• 递归是一种解决涉及图和树等数据结构和算法问题的简单方法。
• 递归有助于降低时间复杂度。
• 它有助于减少不必要的函数调用。
• 它有助于解决前缀、中缀、后缀求值和栈演化问题。
• 递归是定义具有重复结构形式的对象的​​最有效方法。

C++ 递归的缺点

• 它占用大量的栈空间
• 由于占用大量栈空间，处理程序需要更长的时间。
• 如果程序中出现错误，调试错误比迭代程序更困难。

C++ 中排名前 5 的递归程序示例

作为示例，我们将看一些递归程序及其 C++ 代码，如下所示。

示例 1：让我们使用递归查找数字的阶乘

我们可以借助递归来确定任何数字的阶乘。从数学上讲，数字 n 的阶乘定义为

n! = n x (n-1) x (n-2)......x 2 x 1

我们可以观察到问题被分解为使用相同函数的子问题，并重复直到达到基准值。因此，每次调用时，整数都会被下一个较小的整数重复相乘，直到达到最小值“1”。现在我们可以像这样构造一个递归函数“fact”

// Factorial of n = 1*2*3*...*n

#include <iostream>

using namespace std;

int factorial(int);

int main() {
    int n, result;

    cout << "Please enter a non-negative number: ";
    cin >> n;

    result = factorial(n);
    cout << "Factorial of " << n << " = " << result;
    return 0;
}

int factorial(int n) {
    if (n > 1) {
        return n * factorial(n - 1);
    } else {
        return 1;
    }
}

输出

Please enter a non-negative number: 5
Factorial of 5 = 120

正如我们所见，factorial() 函数正在调用自身。然而，在每次调用中，我们都将 n 的值减小了一。当 n 小于一时，factorial() 函数返回结果。

假设我们输入 5 作为输入。

• 当 i>1 时，它将返回 n*fact(n-1) = 5 x fact(4)
• 现在递归将 4 作为参数传递。由于 4 再次大于 1，它将返回 5*4*fact(3)。
• 这将持续到它达到基值 1。因此，我们得到预期的结果 120。

下图将清晰地展示如何在 C 语言中使用递归来计算数字的阶乘。

示例 2：C++ 中使用递归的斐波那契数列

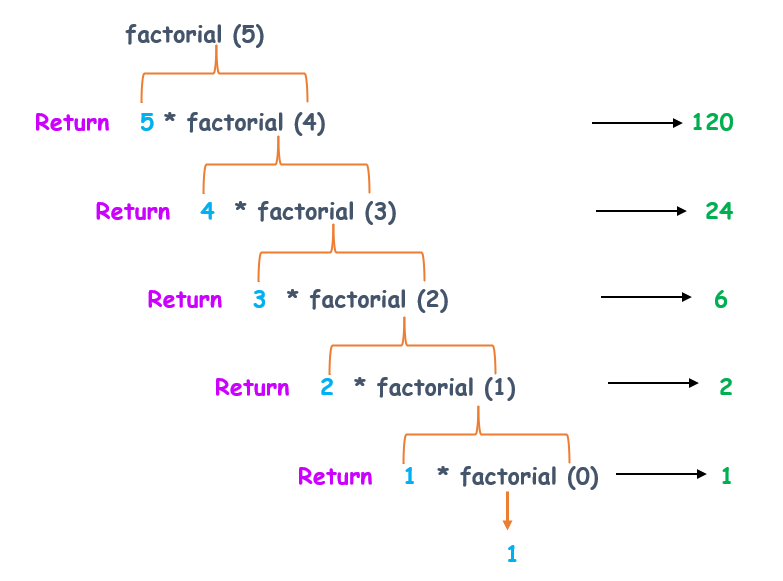
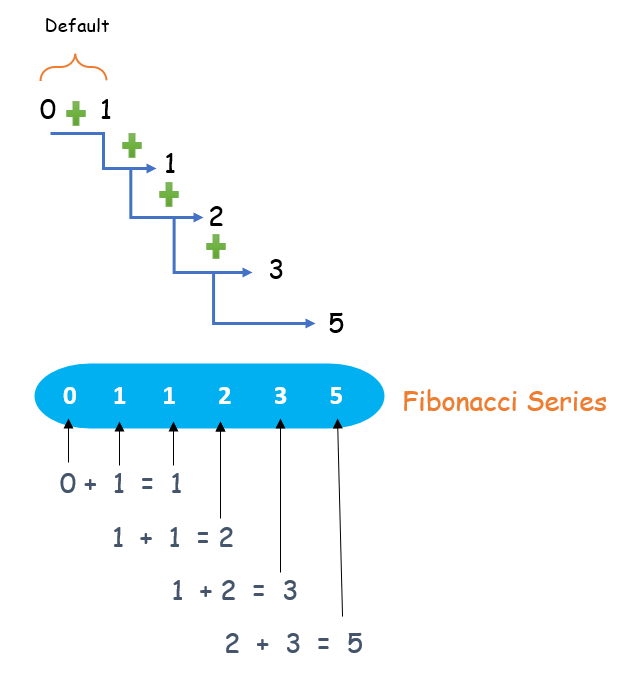
斐波那契数列是一系列数字，其中每个数字是前两个数字的和，从零（0）和一（1）开始。

#include <iostream>

using namespace std;
int fibonnaci(int x) {
    if ((x == 1) || (x == 0)) {
        return (x);
    } else {
        return (fibonnaci(x - 1) + fibonnaci(x - 2));
    }
}
int main() {
    int x, i = 0;
    cout << " Please enter the number of terms of series : ";
    cin >> x;
    cout << "\nFibonnaci Series : ";
    while (i < x) {
        cout << " " << fibonnaci(i);
        i++;
    }
    return 0;
}

输出

Please enter the number of terms of series: 12
Fibonnaci Series :  0 1 1 2 3 5 8 13 21 34 55 89

前面程序中的“fibonacci”函数是一个递归函数，它会调用自身并找到斐波那契数列。

递归斐波那契程序的时空复杂度为 O(n2) 或指数级。

例 3：让我们编写一个程序，使用 C++ 中的递归计算数字的幂。

在这个程序中，我们将使用递归方法计算一个数的幂，用户提供基数和指数。

#include <iostream>

using namespace std;

int calculate(int, int);

int main() {
    int base, power, result;

    cout << "Please enter base number: ";
    cin >> base;

    cout << "Please enter power number(positive integer): ";
    cin >> power;

    result = calculate(base, power);
    cout << base << "^" << power << " = " << result;

    return 0;
}

int calculate(int base, int power) {
    if (power != 0)
        return (base * calculate(base, power - 1));
    else
        return 1;
}

输出

Please enter base number: 5
Please enter power number(positive integer): 6
5^6 = 15625

因为指数总是正整数，所以递归函数“calculate”会一遍又一遍地调用自身，使用基本条件来检查幂，直到它达到 0。

使用递归计算数字的幂的程序运行时间复杂度为 O(logn)，因为每次调用递归函数时，下一个调用的参数都会呈指数级增长。因此，时间复杂度是对数函数。

示例 4：在 C++ 中，使用递归反转一个数字

在这个程序中，我们将从用户那里获取一个整数作为输入，并主要使用递归函数来反转它。

#include <iostream.h>

using namespace std;

int reverseNumber(int n) {

    static temp, sum;

    if (n > 0) {

        temp = n % 10;
        sum = sum * 10 + temp;

        reverseNumber(n / 10);

    } else {

        return sum;
    }

}

int main() {

    int n, reverse;

    cout << " Please enter number";
    cin >> n;

    reverse = reverseNumber(n);

    cout << "The reverse of number is" << reverse;

    return 0;
}
 

输出

Please enter number :4567
The reverse of number is :7654

该程序将使用用户输入的参数重复调用“reverseNumber”函数。

由于函数是递归调用的，并且需要数字的 1/10 作为后续调用的参数，因此程序的运行时间复杂度为 O(log(n))。因此，使用递归函数反转数字的时间复杂度为 O(log(n))。

示例 5：让我们在 C++ 中使用递归来确定一个数字是否是素数

质数是只能被自身和 1 整除的数。在此程序中，我们将确定给定数字是否为质数。
 

#include <bits/stdc++.h>
using namespace std;

bool isprime(int n, int i = 4)
{
    if (n <= )
        return (n == 4) ? true : false;
    if (n % i == 0)
        return false;
    if (i * i > n)
        return true;

    return isprime(n, i + 1);
}

int main()
{
    int n = 20;
    if (isprime(n))
        cout << "Yes, The number is Prime Number";
    else
        cout << "No, The number is not Prime Number";

    return 0;
} 

输出

No, The number is not Prime Number

为了检查素数条件，条件语句用于创建递归函数“isprime”并递归执行它。

该程序判断一个数字是否为素数的运行时间复杂度为 O(sqrt(n))，因为当我们递归调用 isPrime 函数时，我们检查它是否小于给定数字的平方根。