在本篇递归函数教程中,你将掌握关于函数中一种独特过程——递归的一切。此外,你还将看到一些非常适合用递归解决的问题,例如数字阶乘、斐波那契数列等。
与其他编程语言一样,R编程语言中也存在递归函数。当一个函数调用自身时,它就是递归函数。递归有助于将一个大问题(大量的指令集)分解成更小的块。
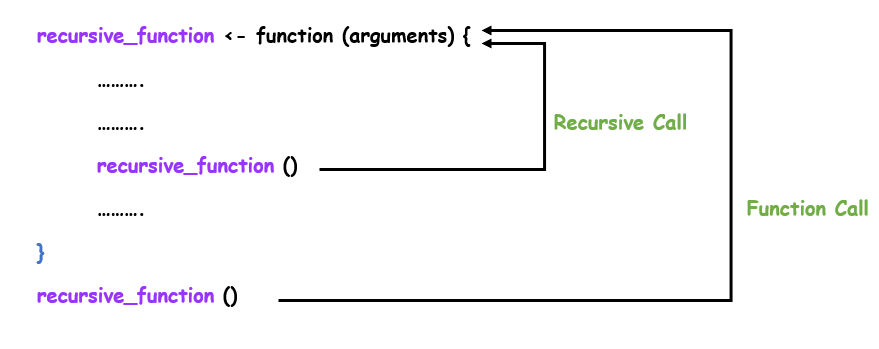
原始函数 (factorial) 在其执行期间在 function() 内部被调用。
递归,通常意味着函数自身重复调用以处理更小问题的过程。如果一个函数调用自身,那么该函数就被称为递归函数,这样的函数调用被称为递归调用。确切地说,当达到基本情况时,递归调用会结束。
在R编程中,递归和迭代相辅相成,但两者都擅长处理为其设计的特定任务。例如,递归对于执行一些数学计算、排序、搜索、遍历等非常有用。然而,它并不适用于所有问题。所以我们可以说它不过是一种自定义函数。一些很适合的问题
在 R 中使用递归是减少代码量的一种优雅方式。
function_name<- function(){ # recursive function
..............
function_name() #recursive call
..............
}
function_name() #function call
R 中递归的工作原理可以最好地可视化如下,以使其更易于理解。
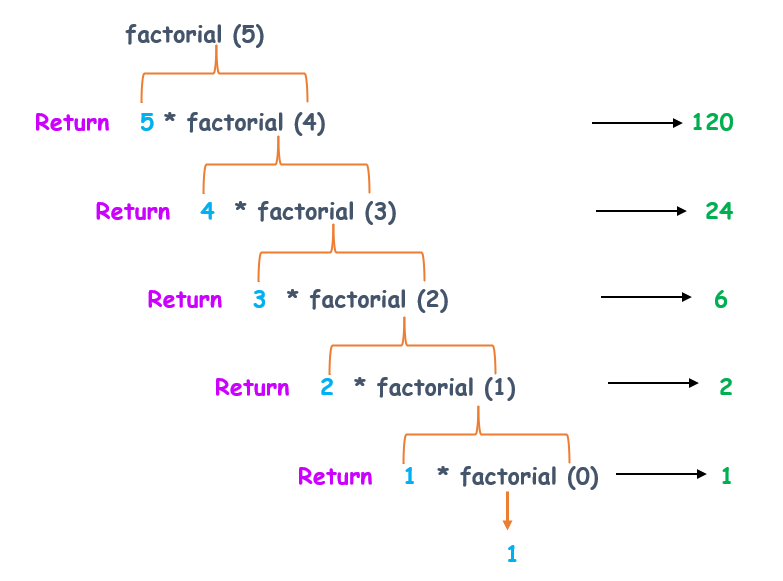
下面是一个简单的R程序,它将通过递归函数找到一个数的阶乘。
factorial<- function(num) {
if(num <= 1) {
return(1)
} else {
return(num * factorial(num-1))
}
}
print(paste("The factorial of 5 is",factorial(5)))
输出将是
[1] "The factorial of 5 is 120"
我们调用函数 factorial(5) 来求 5! 的值,该函数返回一个像 5 x factorial(5-1) 这样的值,即在 factorial 函数内部,它再次用下一个数字 4 调用了同一个函数。这个过程将持续到 factorial(0) 返回 1 为止。最后,每个返回值的乘积将给出答案 120。