


分类与回归树 (CART) 存在一些问题,为了解决这些问题,集成学习中引入了 bagging 和随机森林方法,这有助于提高决策树的准确性。
虽然 CART 是一种直观且强大的算法,但它也存在一些弱点:
为了解决这些问题,已经提出了可以提高决策树准确性的集成方法。我们将讨论两种相关的改进方法:
1. 装袋法 (Bagging)
2. 随机森林
要理解 Bagging,我们需要先了解一种称为自助采样法 (bootstrap sampling) 的统计方法。自助采样法的目标是在数据集大小有限的情况下,估计一个未知的数据分布。
自助采样法 (Bootstrapping) 用于计算总体参数;其工作原理是从数据集中有放回地随机抽取一些数据样本。
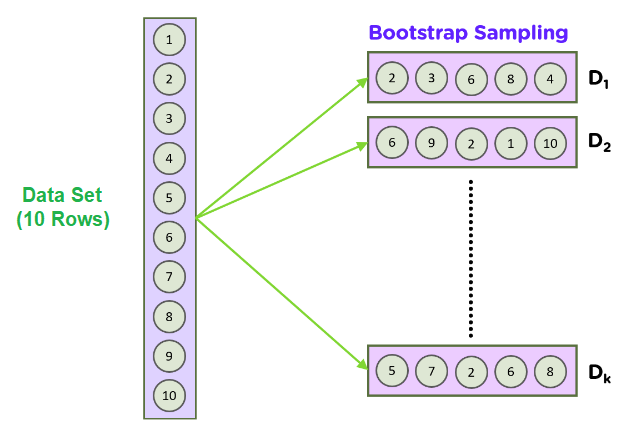
其基本思想是在随机数据采样(即从数据集中取一个较小的子集)时,我们也可以对数据进行重采样:我们从原始数据集中重复抽取样本。这个过程会重复大量次数(1000-10000次),通过计算每次迭代的均值或其他统计量,我们可以了解数据的分布情况。
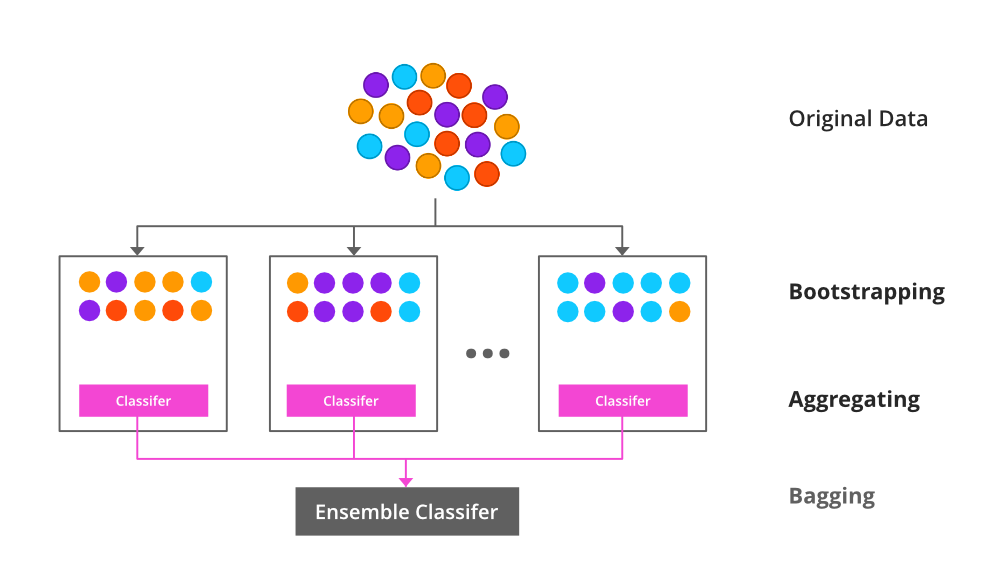
Bagging 也可称为自助聚合 (bootstrap aggregation),它被用于集成学习方法中,以提高集成学习方法的准确性和性能。Bagging 是通过减少数据集中的方差来提高性能的。
Bagging 常用于决策树算法中。它可用于分类和回归方法,因为它有助于减少过拟合问题。
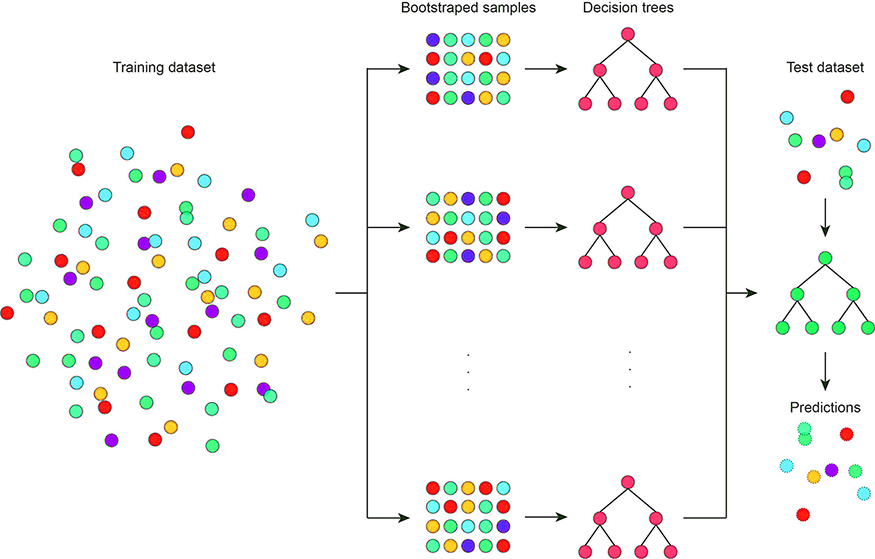
Bagging 旨在使用自助采样法解决 CART 的模型不稳定性问题。Bagging 算法如下:
这个过程稳定了最终模型的答案,因为它选择了在大多数树中都出现的路径。然而,bagging 并没有解决树算法的另一个关键问题:高方差和高度相关的特征。
问题很简单:在构建每棵树时,我们总是使用所有特征。一些特征天然具有较高的方差或彼此高度相关。这些特征在 CART 集成中总是会显示为重要特征,但可能会掩盖数据集中的真实关系。
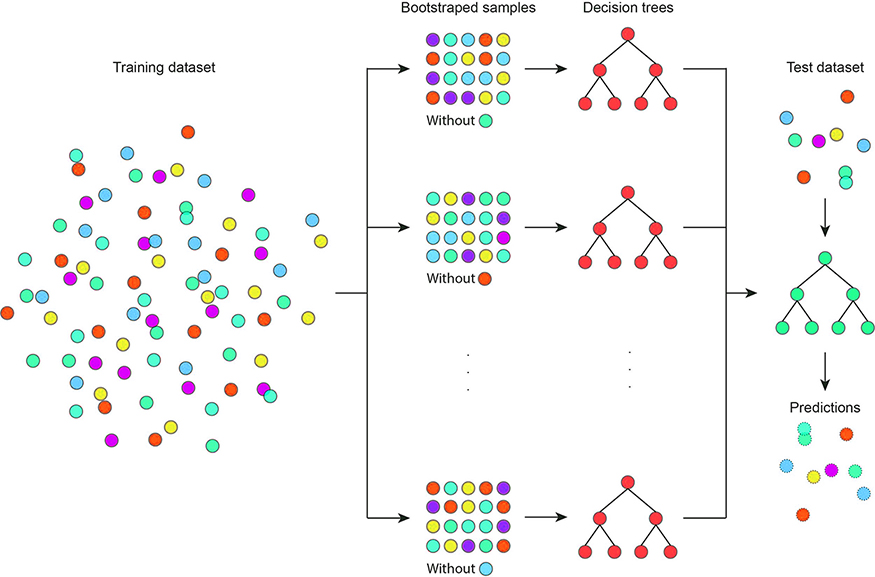
为了解决高方差特征或共线性的问题,一个更好的方法是在 bagging 过程中周期性地省略高变异性特征或移除一些相关特征。这将揭示通常被这些特征隐藏的重要树结构。
随机森林通过对 bagging 过程进行一个微小的调整来解决这个问题:在训练每棵树时,不是使用所有特征,而是使用一个随机且较小的特征子集。这最终会从数据中移除有问题的特征,在多次重复这个过程后,隐藏的树结构就能开始显现。
用于分支分裂的特征数量是随机森林中引入的一个超参数,需要指定。
随机森林是一种带有 CART 模型的自助算法。假设我们有 1000 个观测值和 10 个变量。随机森林将使用这些样本和初始变量构建不同的 CART。它会抽取一些随机样本和一些初始变量来构建一个 CART 模型。然后它会重复这个过程若干次,并预测最终结果,即每个单一预测的平均值。
简单来说,随机森林是随机决策树的集合。但它基于两个概念来从多棵树中得出最终预测。
在每次自助采样过程中,都有一些样本未被包含在模型训练中。这些样本被称为袋外样本 (out-of-bag samples),它们被用作验证集来评估单棵树的模型性能。
通过计算袋外性能的平均值,我们得到了袋装模型的一个估计准确率,这类似于交叉验证过程。这被称为袋外准确率 (out-of-bag accuracy)。
这也是为什么自助采样法对于 CART 和机器学习模型是一种强大的统计方法:它引入了一种稳健的统计方法来评估模型准确性。