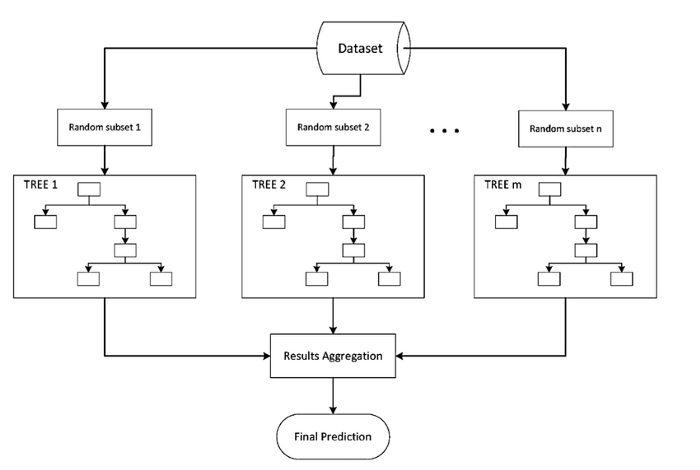
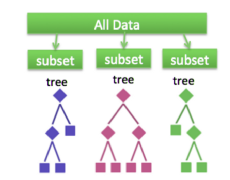
到目前为止,我们一直在讨论单独的机器学习算法,它们本身就具有实际应用,可以扩展到简单的现实问题。然而,当数据集变得更加复杂和庞大时,简单的机器学习算法就开始失效,因为我们对模型施加的假设对于真实和动态的数据来说并不成立。
本教程涵盖集成学习算法,这是一类机器学习算法,通过将多个模型组合在一起形成一个最优模型以获得准确的预测,从而解决这个大型现实数据问题。
现在让我们考虑一个例子,使这个概念更清晰。以决策树为例来理解集成学习的概念。这里我们需要根据输入模型的问题获得预测结果。
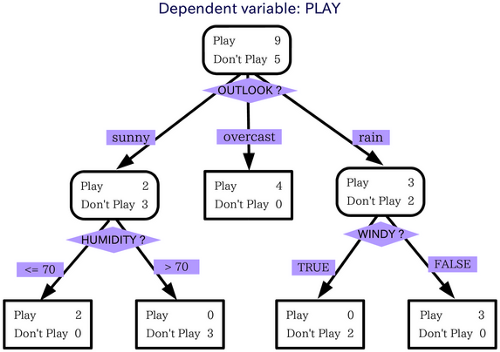
在这个例子中,我们考虑的问题是:我们能在雨中出门吗?为此,决策树会考虑许多因素,并为每个因素做出决定或提出另一个问题。所以当你查看上面的图片时,你会明白如果情况是阴天,我们就可以出门。
如果下雨,我们必须询问是否有风。如果有风,我们不能出门,否则就可以出门。同样,当阳光明媚时,我们必须询问湿度是否很高。并根据此做出决定。
如果我们使用集成方法,事情会更方便。集成方法可以自由地使用决策树的小模型,计算要选择的特征以及在每个决策分割中要提出的问题。
集成学习算法结合多个算法来解决复杂问题。它们类似于一家公司,由擅长各自领域的专家组成,以解决复杂的现实问题。以战略方式组合算法可以比单个回归器或分类器具有更好的性能。
然而,需要注意的是,并非所有集成方法都会优于一个简单的、训练良好的模型。相反,我们可以将集成学习模型视为一种风险缓解策略。我们不必满足于一个训练不佳的模型,而是可以结合多个不同回归器和分类器的结果,以至少获得一个表现不错的模型。
值得注意的是,许多机器学习算法产生的预测结果都依赖于初始起始条件。例如,K-均值聚类取决于簇的数量以及这些质心的初始化位置。
在任何给定的迭代中,即使我们保持超参数值不变,这些模型的预测也可能发生变化。这被称为模型稳定性,拥有一个对这些不同初始条件具有鲁棒性的模型非常重要。
集成方法倾向于提供稳定的模型预测。这是因为模型输出被组合,通常通过对多个回归器的结果进行平均或对不同分类器进行多数投票。生成的模型越多,由于大数定律,该值就越稳定。
集成模型结合了具有不同假设和超参数的不同模型。因此,它们可以捕获数据集中存在的更多方差。这意味着与更简单的模型相比,它们可以识别数据中更多的非线性趋势。
集成学习模型的一个主要缺点是,由于它们更复杂,它们变得像黑盒子——识别模型错误的来源以及模型如何得出结论变得更加困难。
由于集成模型捕获了更多的数据方差,它们更容易受到数据中的噪声和过拟合的影响。缓解这个问题的一种方法是应用正则化技术并采样合适的超参数,以最好地捕获数据趋势。
然而,我们还将在即将到来的教程中讨论解决模型过拟合问题的算法特定方法。