


线性回归是一种对特征(称为自变量或输入变量)与响应或输出(即因变量)之间关系进行建模的方法,这些因变量是给定一组输入特征的。
线性回归是用于回归分析的最常见和最流行的机器学习算法之一。线性回归使用统计方法,输出将是实数和连续的,用于预测销售额、年龄、产品价格预期等。
这种方法的主要假设是模型旨在学习的参数或系数是直线。
一个简单的示例如下所示
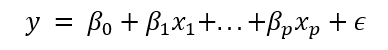
其中 p 是数据集中预测变量的数量,β0 是截距,βp 表示我们试图用给定特征 xp 估计的参数。
ε 是残差:表示直线与实际数据点之间的偏差。这个变量很重要,因为它是衡量模型错误程度的指标。残差平方和或RSS是用于评估模型拟合度的度量标准。
线性回归将有助于可视化输入变量与预测输出之间的关系,这种关系将是线性的,即直线,因此我们称之为线性回归。
在线性回归的图形表示中,独立的输入变量将在 X 轴上,而依赖的输出变量将在 Y 轴上,线性回归将是一条连接最大数据点的倾斜直线。
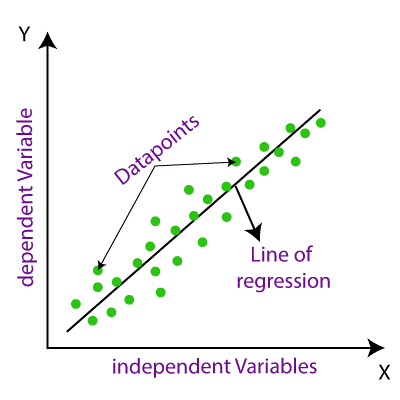
在此图形表示中,我们可以理解线性回归如何表示为连接最大数据点的直线。
请注意,虽然模型参数 β 与预测变量 x 之间的关系需要是线性的,但非线性函数可以应用于数据。以下方程将被视为线性回归问题,尽管它更复杂
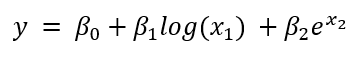
以下方程是一个非线性函数,因为参数与预测变量不成比例。
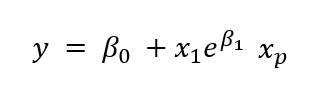
在回归分析教程中,我们已经提到线性回归可以再次分为两种
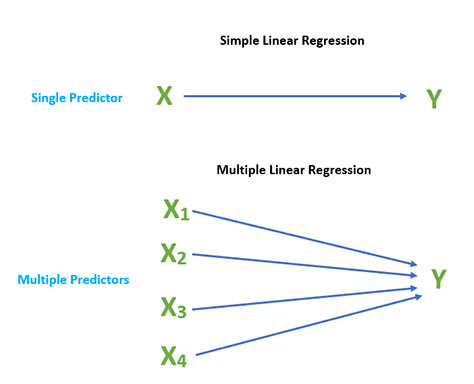
如果我们只有一个独立输入变量来确定输出,我们将此类机器学习算法称为简单线性回归。
我们可以简单地说它为
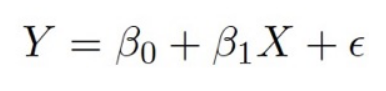
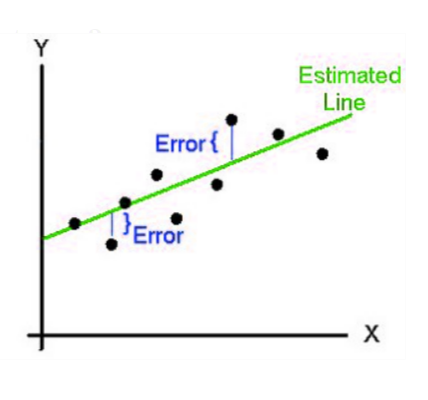
在此图形表示中,我们可以理解简单的线性回归如何表示为连接数据点的直线。
多元线性回归与简单回归相反,如果我们有一个以上的输入预测变量来确定依赖的输出变量,我们将此类机器学习算法称为多元线性回归。输入变量可以是连续的或分类的。
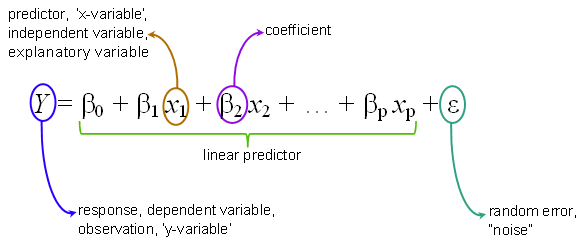
描述多元线性回归方程中预测值与自变量之间关系的方程
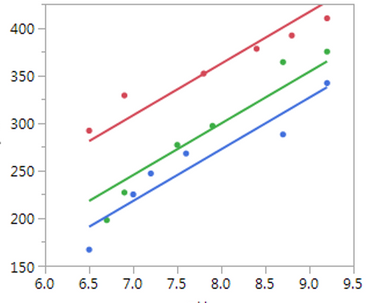
上图显示了在同一图上绘制多条线性回归线
在线性回归图中,我们知道有一条直线关联着输入变量和预测变量之间的关系,这条直线被称为线性回归线。在这张图中,线性回归线可以向我们展示两种不同的关系,它们是:
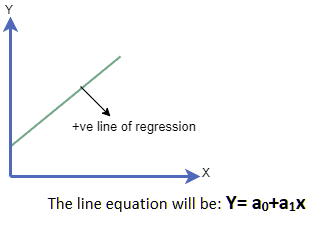
在线性回归图中,如果输入自变量和预测输出变量都分别沿 x 轴和 Y 轴增加,则称为正向关系。
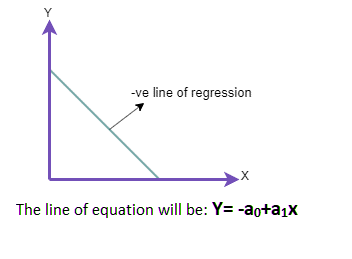
在线性回归图中,如果输入变量沿 x 轴增加,而依赖于独立输入变量的预测输出变量沿 Y 轴减少,并且回归线将在某一点与 y 轴相交。这称为负线性关系。
模型性能可以描述为回归线与数据点之间的关系,它们接触的程度,以及与回归线的距离。我们必须从回归中的不同模型中找到最佳模型,这称为模型优化,可以通过以下方式完成:
这是一种简单的统计方法,用于确定回归线与图中数据点的拟合程度。R 平方方法通过计算输入和输出变量之间关系的强度,以 10 到 100 的百分比范围表示。
R 平方值用于确定模型的完美程度。R 值高意味着模型很好,因为它表示预测值与真实值之间的差异较小。这也称为决定系数。
我们可以使用以下公式计算 R 平方值
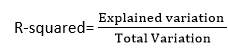
训练回归模型最常用的方法是最小二乘法。该模型旨在最小化每个数据点到表示 x 和 y 之间关系的直线之间的平方误差之和。
在数学上,我们可以将这种关系写成以下语句
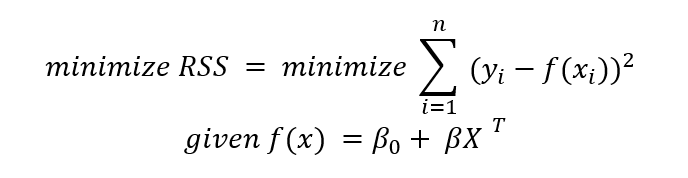
最小二乘回归是一个相对简单的模型。我们试图找到最能拟合数据的直线,同时最小化模型的误差。
那么我们为什么要使用最小二乘法处理真实数据呢?
波士顿房价数据集是一个经典数据集,包含与波士顿房地产市场相关的几个特征,包括犯罪率和 1978 年房屋中位价。
此数据集的目标是预测房屋的中位价格。
我们将特征和目标数据集设置为 Pandas 数据帧数据类型,以便于后续分析。
# Import general-use data science libraries
import pandas as pd
import numpy as np
# Import features
df = pd.DataFrame(data=data.data,
columns=data.feature_names)
print(df)
# Import target (median housing prices)
target = pd.DataFrame(data=data.target,
columns=["MEDV"])
print(target)
CRIM ZN INDUS CHAS NOX ... RAD TAX PTRATIO B LSTAT
0 0.00632 18.0 2.31 0.0 0.538 ... 1.0 296.0 15.3 396.90 4.98
1 0.02731 0.0 7.07 0.0 0.469 ... 2.0 242.0 17.8 396.90 9.14
2 0.02729 0.0 7.07 0.0 0.469 ... 2.0 242.0 17.8 392.83 4.03
3 0.03237 0.0 2.18 0.0 0.458 ... 3.0 222.0 18.7 394.63 2.94
4 0.06905 0.0 2.18 0.0 0.458 ... 3.0 222.0 18.7 396.90 5.33
.. ... ... ... ... ... ... ... ... ... ... ...
501 0.06263 0.0 11.93 0.0 0.573 ... 1.0 273.0 21.0 391.99 9.67
502 0.04527 0.0 11.93 0.0 0.573 ... 1.0 273.0 21.0 396.90 9.08
503 0.06076 0.0 11.93 0.0 0.573 ... 1.0 273.0 21.0 396.90 5.64
504 0.10959 0.0 11.93 0.0 0.573 ... 1.0 273.0 21.0 393.45 6.48
505 0.04741 0.0 11.93 0.0 0.573 ... 1.0 273.0 21.0 396.90 7.88
[506 rows x 13 columns]
MEDV
0 24.0
1 21.6
2 34.7
3 33.4
4 36.2
.. ...
501 22.4
502 20.6
503 23.9
504 22.0
505 11.9
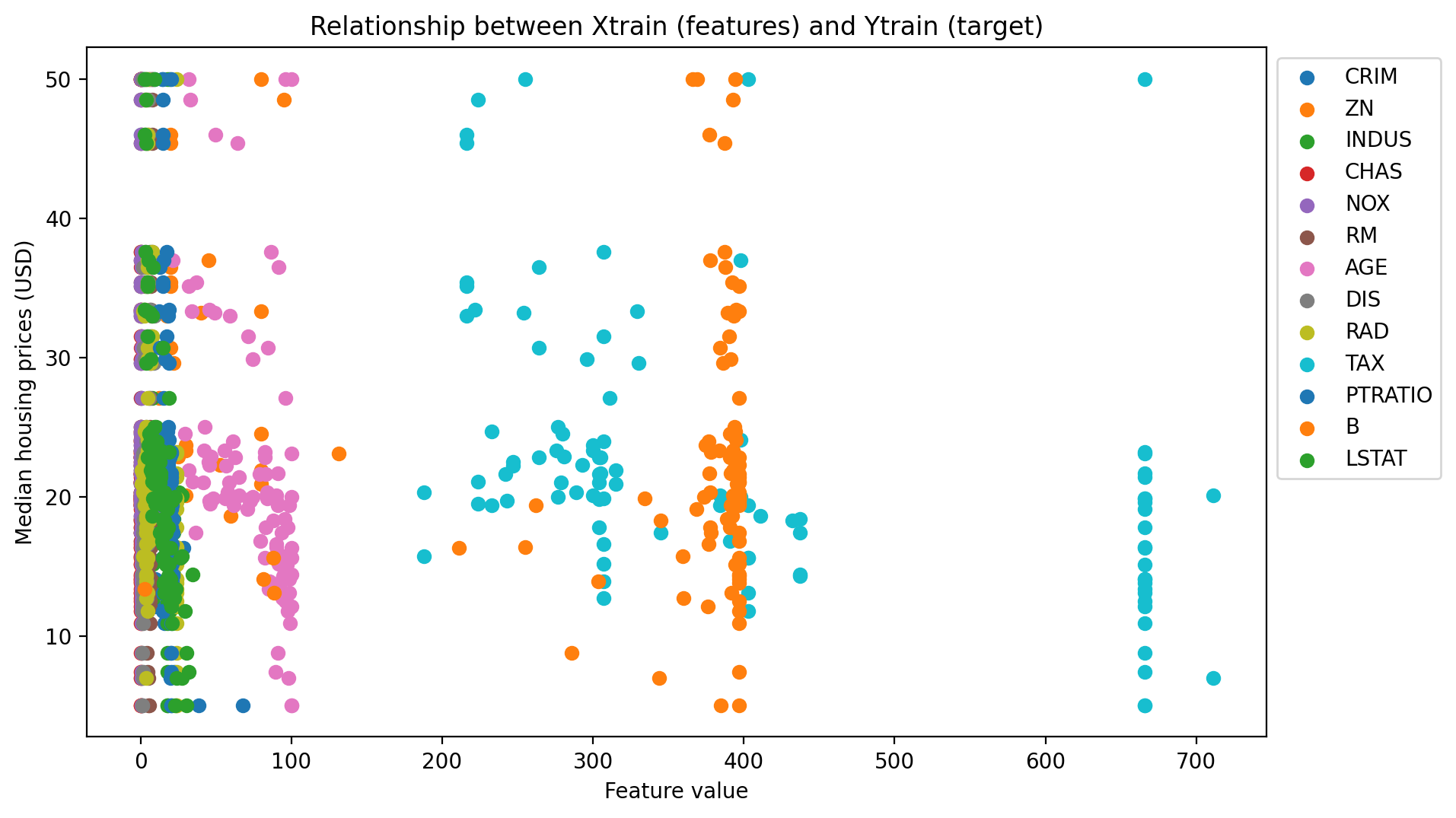
from matplotlib.pyplot import figure
fig, ax = plt.subplots()
for i in Xtrain:
plt.scatter(Xtrain[i], Ytrain, label=str(i))
ax.legend(bbox_to_anchor=(1., 1.))
plt.xlabel("Feature value")
plt.ylabel("Median housing prices (USD)")
plt.title("Relationship between Xtrain (features) and Ytrain (target)")
fig.set_dpi(200)
savepath="/content/img/"
fig.set_size_inches(10, 6)
fig.savefig(savepath+"scatter.png", bbox_inches='tight')
Dataset sizes after train_test_split() Xtrain size: (101, 13) Xtest size: (405, 13) Ytrain size: (101, 1) Ytest size: (405, 1)
from matplotlib.pyplot import figure
fig, ax = plt.subplots()
for i in Xtrain:
plt.scatter(Xtrain[i], Ytrain, label=str(i))
ax.legend(bbox_to_anchor=(1., 1.))
plt.xlabel("Feature value")
plt.ylabel("Median housing prices (USD)")
plt.title("Relationship between Xtrain (features) and Ytrain (target)")
fig.set_dpi(200)
savepath="/img/"
fig.set_size_inches(10, 6)
fig.savefig(savepath+"scatter.png", bbox_inches='tight')
# Fit the model
from sklearn.linear_model import linear_model as lm
model = lm().fit(Xtrain, Ytrain)
print(model)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
print("Important model objects")
print("Regression coefficients: ", str(model.coef_))
print("Y-intercept: ", str(model.intercept_))
Important model objects Regression coefficients: [[-1.10998550e-01 5.59525865e-02 1.52041041e-01 1.62336940e+00 -2.52970054e+01 3.14436742e+00 3.94375733e-02 -1.31328247e+00 3.01518760e-01 -1.20457172e-02 -1.23308582e+00 6.49058329e-03 -6.06938545e-01]] Y-intercept: [47.50246908]
模型对象有几种关联方法。如果我们要用测试集进行预测,可以使用 predict() 方法。
Ypred = model.predict(Xtest)
print(Ypred)
[21.04711236] [16.0519687 ] [22.08124826] [24.9550908 ] [22.58486361] [18.30309637] [36.34589925] [20.84835474] [34.53960168] [25.75900913] [18.57619619] [ 3.15134125] [24.60956537] [18.28628001] [15.22482753] [29.71273752] [31.22651416] [22.66172954] [20.61047944] [22.90176779] [26.96548001] [19.92578633] [31.0290531 ] [19.55288498] [19.0799543 ] [23.47680399] [18.14110649] [14.52089098] [27.04951364] [25.58432198] [22.15694304] [21.72038631] [20.88291021] [18.1170226 ] [19.05318278] [30.97678281] [30.5478923 ] [16.62990827] [18.75101055] [33.66266989] [17.01643957] [14.17095253] [32.62854346] [24.94957009] [13.37233271] [24.45143619] [20.09491092] [38.58474904] [44.15771256] [21.54061052] [21.61272714] [ 3.85894539] [19.81522043] [42.8604927 ] [26.02782308] [35.09436136] [23.79821583] [18.26944428] [32.92705099] [14.8280985 ] [20.77294734] [12.31289156] [34.24357418] [22.66837597] [13.22221194] [21.63774045] [17.37198566] [17.85270836] [30.28365937] [32.18075657] [20.45336081] [29.75959666] [ 7.18982288] [18.89723132] [30.10475681] [20.57839242] [33.3974039 ] [24.24358861] [14.26738546] [24.20106907] [32.91401148] [17.80684621] [26.29527134] [22.10605813] [24.43018928] [32.65649583] [26.2304317 ] [23.11068013] [21.37121057] [21.59383797] [11.26008499] [16.94212371] [22.85497267] [29.61466174] [23.09151181] [12.26582213] [24.38136745] [13.14379108] [ 7.98377975] [31.77241579] [12.00109812] [13.18440467] [31.33628903] [19.70216857] [28.20054128] [ 0.60101149] [31.12712135] [24.19502058] [29.53687253] [ 9.68649156] [10.11971136] [ 7.12036418] [20.70524276] [14.50594171] [23.88299493] [22.20130119] [ 6.58848017] [18.23088525] [30.87930596] [14.74069658] [22.10694463] [32.68525461] [29.82819265] [30.72089238] [19.16986842] [29.39425529] [17.80744526] [21.82646237] [24.31193619] [30.23574889] [20.25455558] [15.88697828] [23.44452457] [21.86141303] [14.83881915] [32.36894068] [23.76741903] [21.66801612] [13.53616923] [16.77326467] [16.68268242] [33.67449135] [30.06984231] [25.98382116] [15.58993356] [17.51342189] [ 5.72952529] [12.49735596] [27.35548835] [35.55403582] [26.03031409] [30.2652679 ] [20.79109449] [13.36025789] [25.72460123] [ 8.9366379 ] [15.54265181] [25.21990601] [18.55971622] [32.15802211] [36.40020073] [22.56136319] [22.7234512 ] [34.37231992] [-3.94468944] [14.23851594] [20.31829917] [32.69907633] [21.14937346] [27.1818681 ] [20.77005275] [26.33401396] [18.66135437] [29.2236251 ] [32.13618142] [13.65673552] [ 9.83952335] [37.20348635] [20.45829063] [18.82696886] [22.46200016] [20.70769228] [24.98878401] [24.94873464] [22.63186389] [27.95664184] [34.95321661] [29.57340438] [ 6.2979752 ] [18.58409807] [22.12319937] [21.82862584] [12.68613277] [11.81831775] [23.86158832] [24.73085406] [30.67013986] [24.06240533] [34.82481321] [18.24315249] [15.27193751] [11.26864556] [31.03156474] [27.71373401] [41.03106415] [28.29517411] [19.41491991] [36.25536337] [21.12170882] [32.81354451] [24.64850689] [31.94774974] [19.8091977 ] [17.03760649] [28.82566707]]
然后我们可以计算 MSE。
mse = np.square(np.mean(Ytest-Ypred))
print(mse)
MEDV 0.139942 dtype: float64
如果我们想衡量直线与测试数据集的拟合程度(又称决定系数),我们可以使用 score() 方法。
R2 = model.score(Xtest, Ytest)
print(R2)
0.7219648298245812
决定系数的值介于 0 和 1 之间,其中 1 表示完美拟合。我们有一个相当不错的分数!