


在机器学习中,我们关注的是找到一个函数,它能最好地映射某些数据与结果之间的关系。我们通常关注模型预测与实际标签或数据值相比的准确性。为此,我们需要设定一个程序来最大化给定类别的概率或最小化模型误差。这被称为优化问题。
在本教程的其余部分,我们将讨论最常见的优化用法,即最小化模型误差或成本值。计算模型误差的函数称为成本函数。
成本函数告诉模型在映射输入数据和输出关系时模型有多大的错误。这是通过一个称为成本值的单一值来衡量的,它代表预测值和实际值之间的平均误差。
既然我们有了衡量模型误差的方法,接下来我们需要讨论如何最小化成本函数。我们将使用的优化过程称为梯度下降,它是一种高效的优化算法,用于神经网络等多种模型。该算法试图找到与给定模型相关的最小误差。
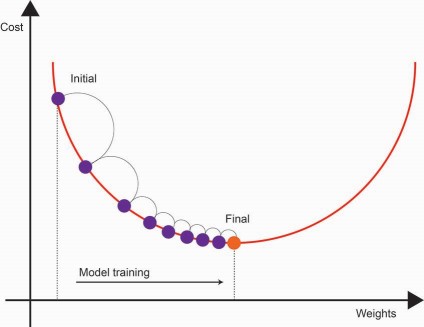
模型训练以逐步的方式进行,经过多次迭代。直观地说,梯度下降试图找到模型应该调整其系数的方向,以在每一步中减少误差。这个方向被称为梯度。
随着我们不断地通过每次迭代训练模型,成本值逐渐收敛到最小值。此时,成本值趋于稳定。在每一步中,模型系数都会由梯度进行调整,从而最小化成本函数。
既然我们已经讨论了为什么需要计算成本值,接下来我们将讨论一些常见的成本函数。
均方误差 (MSE) 是一个相对直观的函数,用于估计误差的平均平方。平方项强制值为正,其中值越接近0表示模型误差越小。这个成本函数通常应用于基于回归的任务。
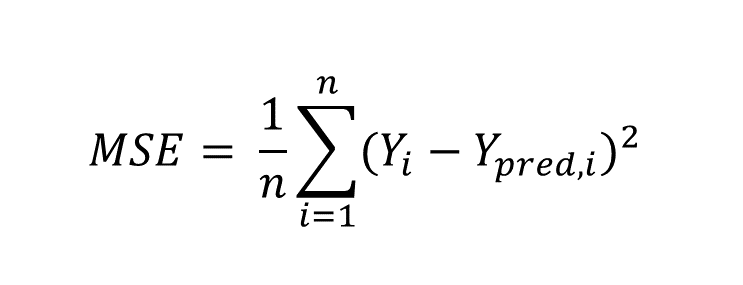
交叉熵是通常应用于分类任务的成本函数,其根源在于逻辑回归。交叉熵源自信息论,并衡量两个概率分布对于一个随机变量的不同程度。

如果我们将此推断为二分类问题,平均交叉熵表达式将如下所示:
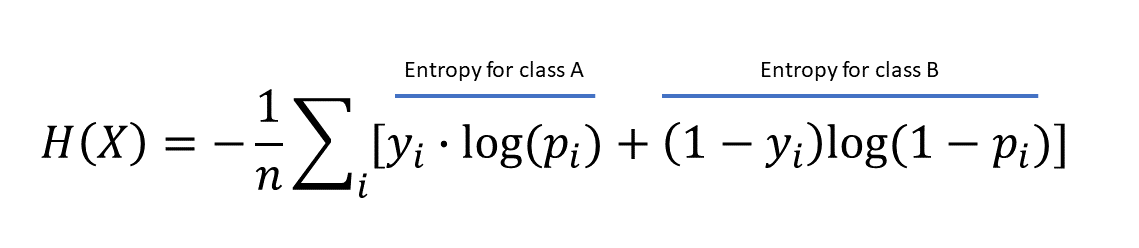
交叉熵损失值的解释如下。如果值为0,则预测的类别概率与实际集合完全相同。然而,如果值较高,则预测标签与实际数据之间的概率分布存在一定距离。
上面的例子是交叉熵损失函数的二分类方程。但是,如果类别超过2个呢?
目前暂不深入太多技术细节,我们可以将上述损失函数推广以考虑多类别逻辑回归问题。Softmax函数是多项逻辑回归的扩展(稍后将详细介绍)。但它使用相同的交叉熵损失函数来评估观察值属于给定类别的概率。