


支持向量机是最流行和常用的监督机器学习算法之一,主要用于分类,但也可用于分类和回归类型问题。它因其良好的准确性和较低的计算成本而广受欢迎。
我们知道,分类是将数据分为不同的类别,我们需要有一条清晰精确的线来将数据分类,支持向量机通过创建一条清晰的边界线来做到这一点,我们称之为超平面。借助这条边界线,我们可以轻松地将新数据分类到不同的类别中。
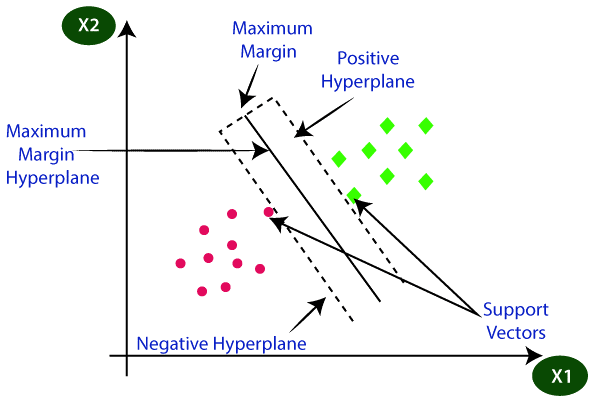
超平面是借助支持向量创建的。支持向量是我们选择来创建超平面的极端点。我们使用这些支持向量来决定超平面,因此我们将此机器学习算法称为支持向量机。
从下图中,您可以理解超平面以及根据超平面划分的类别。
现在让我们通过一个简单的例子来进一步阐明。假设我们有一些老虎和狮子,我们有一只奇怪的老虎,它与狮子有一些相似之处。在这种情况下,我们需要一个能够清楚地区分老虎和狮子的模型。为此,我们需要支持向量机的帮助,它将通过大量老虎和狮子的图像进行训练,以便能够正确地对狮子和老虎进行分类。
现在我们将这只奇怪的老虎展示给支持向量机,它通过选取老虎和狮子中的极端点来创建超平面,然后在这两者之间建立决策,最后根据支持向量和超平面将这只奇怪的老虎归类为老虎。
支持向量机的主要应用领域是人脸检测、图像分类等。
首先,我们来看下面的二元分类问题示例,该问题旨在识别实心和空心数据点之间的决策边界
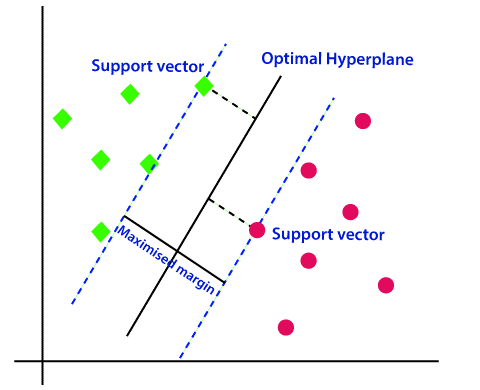
**支持向量**是距离**决策边界**(实线)最近的数据点。它们是最难分类的数据点,并直接决定决策边界的位置。
目标:最大化两类之间的间隔
支持向量机旨在最大化不同类别的支持向量之间的间隔(虚线)。换句话说,我们试图找出如何识别能够最好地分离数据的决策边界。
它是如何最大化间隔的?它通过**约束优化**方法实现这一点——这些方法根据我们定义的表示限制的约束来优化一些目标函数。
理解优化步骤的数学需要大量的线性代数知识,但在本教程的其余部分,我们将只解释支持向量机的直观概念。一般来说,支持向量机可以分为两种类型:
线性支持向量机用于简单数据集,其中数据点可以使用一条线性线分类为两类。此类数据点称为线性数据,此类算法称为线性支持向量机分类器。
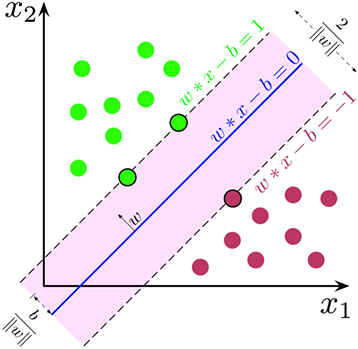
对于线性支持向量机,目标是绘制一条最能将两类分开的直线,这通过以下方式实现:
虽然我们已经展示了类之间完美分离的突出示例,但我们应该注意,有时我们需要接受一些错误。毕竟,如果支持向量机总能完美地分离数据,那它就会过拟合,无法推广到其他数据集。支持向量机旨在最大化数据点的分离,并允许一些错误的数据点被分类。
假设我们有一个包含绿色和粉色点数据的数据集。因此,我们需要一个能够根据x和y坐标对绿色和粉色点进行分类的算法,其中x和y是数据集的特征。
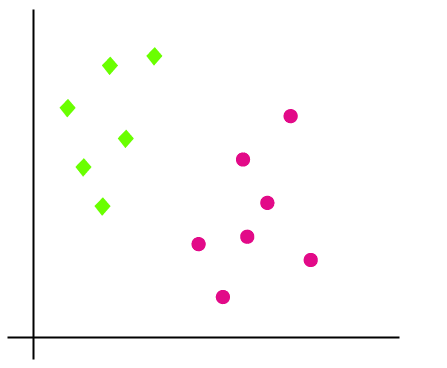
现在让我们检查一下,它是一个二维平面,我们可以使用一条直线分离数据点并将其分为两类,但在这种情况下,我们可以绘制多于一条直线,就像这张图片一样。
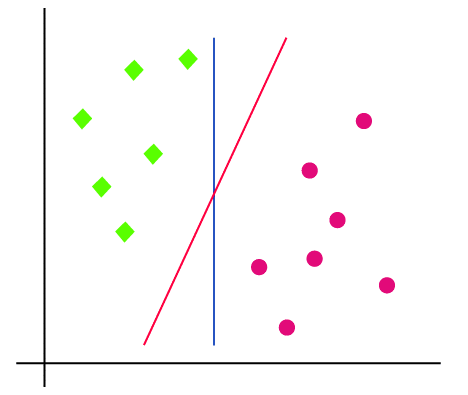
所以问题来了,哪条线将是分类数据点的完美线,这就是支持向量机的作用。支持向量机有助于绘制最佳线,称为超平面。在找到被称为决策边界的线之后,支持向量机将找到两个类别中距离超平面最近的点,这被称为支持向量。现在,超平面和支持向量之间将存在一个间隙,这被称为间隔。支持向量机的主要目标是最大化间隔,它将被称为最优超平面。
非线性支持向量机用于非线性数据,这意味着数据集不能用线性线划分。我们用来对非线性数据进行分类的这类算法称为非线性支持向量机。
假设原始数据本身不是线性可分的。解决这个问题的一种方法是通过将数据投影到更高维空间来使其线性可分。为了可视化这意味着什么,假设我们有两个类之间有以下数据分布。
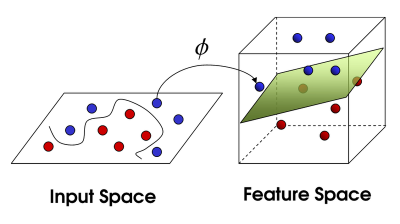
左侧的数据分布很难在二维平面上使用线性模型进行建模。然而,如果我们将数据通过函数扩展到更高的维度,就有可能绘制一个**超平面**来分离紫色和橙色点。
这种为数据集增加维度的强大方法称为**核函数**。许多核函数可以应用于不同的数据结构,它是一个需要考虑的超参数,以优化支持向量机模型。
1. 支持向量机提供高精度
2. 支持向量机在所有维空间中表现良好
3. 支持向量机使用的内存和资源非常少
4. 成本效益高
1. 训练时间长,不适用于大数据
2. 如果数据类别重叠,则会失败或给出错误预测
1. 面部观察和检测
2. 文本和超文本安排
3. 生物信息学