


在上一节课中,我们讨论了线性回归,它是一条连接因变量和非因变量的直线,但并非总是能用这条直线进行线性拟合。然后引入了多项式回归来建模非线性函数。然而,我们讨论过,添加的多项式项越多,模型就越容易过拟合。
为了拟合描述真实数据的复杂形状,我们需要一种方法来设计复杂的函数而不会过拟合。为此,我们必须提出一种新的方法,它是一种非线性回归,但结合了线性和非线性函数来拟合数据点,这被称为回归样条。
为了克服线性回归和多项式回归的缺点,我们引入了回归样条。正如我们所知,在线性回归中,数据集被视为一个整体,但在样条回归中,我们必须将数据集分成许多部分,我们称之为bin。我们划分数据的点称为节点(knots),我们会在不同的bin中使用不同的方法。我们在不同bin中使用的这些独立函数称为分段阶梯函数。
样条是一种通过将其分解为较小的分段多项式函数来拟合高次多项式函数的方法。对于每个多项式,我们拟合一个独立的模型并将它们全部连接起来。
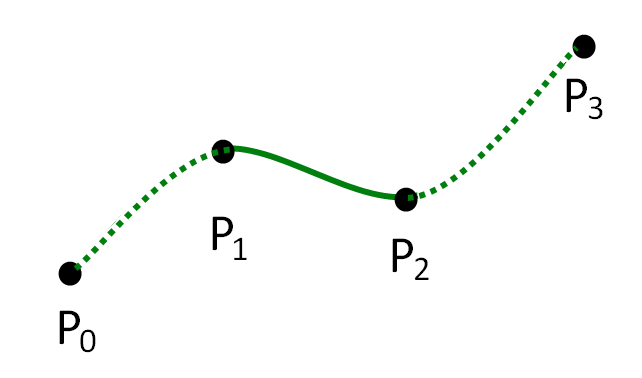
我们已经讨论过,线性回归是一条直线,因此我们引入了多项式回归,但它可能导致模型过拟合。对一种既具有线性回归的良好特性又具有多项式回归良好特性的模型的需求促使了样条回归的诞生。虽然这听起来很复杂,但通过将每个部分分解为较小的多项式,我们降低了过拟合的风险。
由于样条将多项式分解为更小的部分,我们需要确定在哪里分解多项式。发生这种划分的点称为节点(knot)。
在上面的例子中,每个P_x代表一个节点。曲线两端的节点称为边界节点,而曲线内的节点称为内部节点。
虽然我们可以通过目视检查来确定这些节点的位置,但我们需要设计系统的方法来选择节点。
一些策略包括
如果没有微积分和分段函数的一些性质知识,样条的数学原理可能看起来很复杂。我们将讨论这些算法背后的直觉。
如果您对样条的具体数学原理感兴趣,我们可以向您推荐 Trevor Hastie、Rovert Tibshirani 和 Jerome Friedman 的《统计学习要素(第2版)》。这本中高级教材是志向远大的数据科学家的必读之物。
三次样条要求我们平滑地连接这些不同的多项式函数。这意味着这些函数的一阶和二阶导数必须是连续的。下面的图显示了三次样条以及一阶导数如何是连续函数。

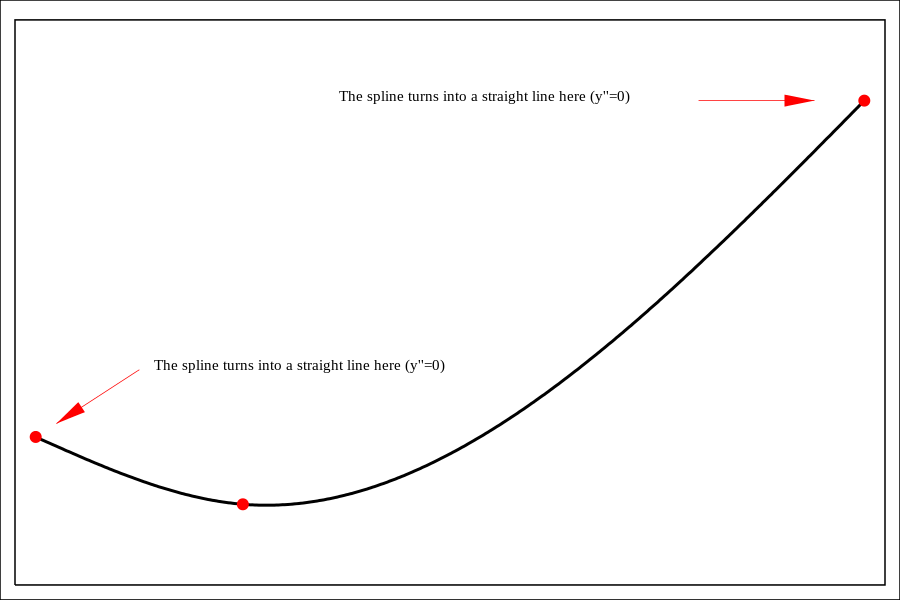
多项式函数和其他类型的样条往往在函数的末端拟合不佳。这种可变性可能会产生巨大的后果,尤其是在预测中。自然样条通过强制函数在边界节点之后保持线性来解决这个问题。
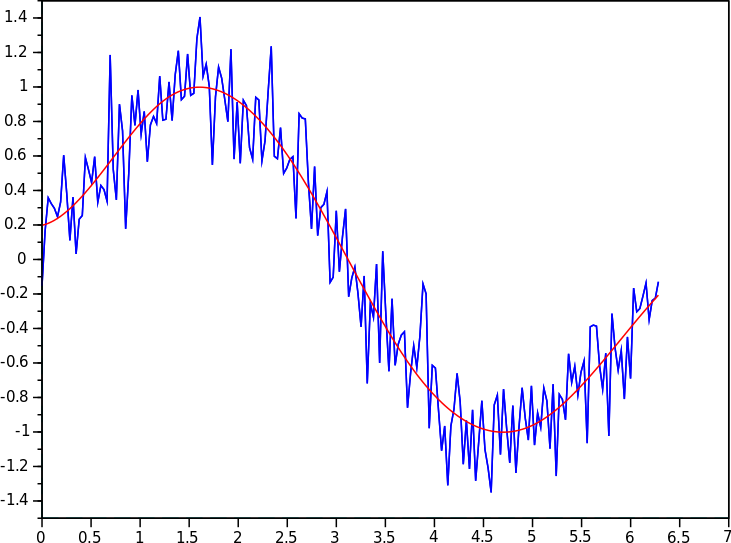
最后,我们可以考虑样条的正则化版本:平滑样条。如果系数的可变性很高,则会惩罚成本函数。下图显示了需要平滑样条才能获得足够模型拟合的情况。
要在 Python 中实现样条,您可以使用 SciPy 库。这里可以找到一个有用的示例。
import matplotlib.pyplot as plt
from scipy.interpolate import UnivariateSpline
rng = np.random.default_rng()
x = np.linspace(-3, 3, 50)
y = np.exp(-x**2) + 0.1 * rng.standard_normal(50)
plt.plot(x, y, 'ro', ms=5)
spl = UnivariateSpline(x, y)
xs = np.linspace(-3, 3, 1000)
plt.plot(xs, spl(xs), 'g', lw=3)
spl.set_smoothing_factor(0.5)
plt.plot(xs, spl(xs), 'b', lw=3)
plt.show()
输出
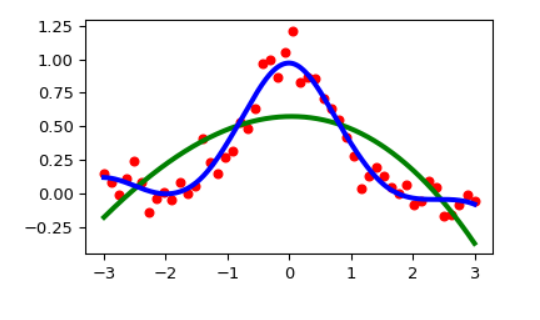
我们已经介绍了许多常用的非线性回归模型。在每种情况下,我们发现函数往往是线性模型的变体,但我们堆叠了不同层次的复杂性。广义加性模型(GAM)可以被视为对目前所涵盖方法的概括。
对于目前描述的每种回归方法,我们都添加了每个特征xi 对预测某个结果yi 的贡献。
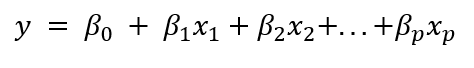
在目前描述的所有情况下,我们都强制βp 和 xp 之间的关系是线性的。多项式回归也是如此——我们只是将 xp 的上标更改为最能映射到 y 的值。
使用 GAMs,我们断言我们可以向模型添加任何我们想要的函数,并通过将这些函数相加来预测 y。
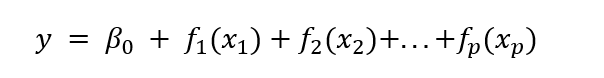
其中函数 f_p 可以是任何将 y 与 x_p 关联起来的线性/非线性函数。由于该函数连接 x 和 y,因此它被称为连接函数。
GAMs 功能强大,易于解释,这得益于模型的加性性质和框架中内置的灵活性。此外,该方法经过正则化以避免过拟合,增加了 GAMs 在复杂回归任务和预测中的吸引力。
GAMs 可以使用 statsmodels 库实现。