正则化

我们已经讨论过机器学习模型的过拟合问题，它会导致模型做出不准确的预测。这将影响模型的效率。

什么是正则化？

正则化是解决过拟合问题的方法。我们可以说，正则化通过向模型添加更多信息来防止模型的过拟合问题。

什么是机器学习模型的过拟合？

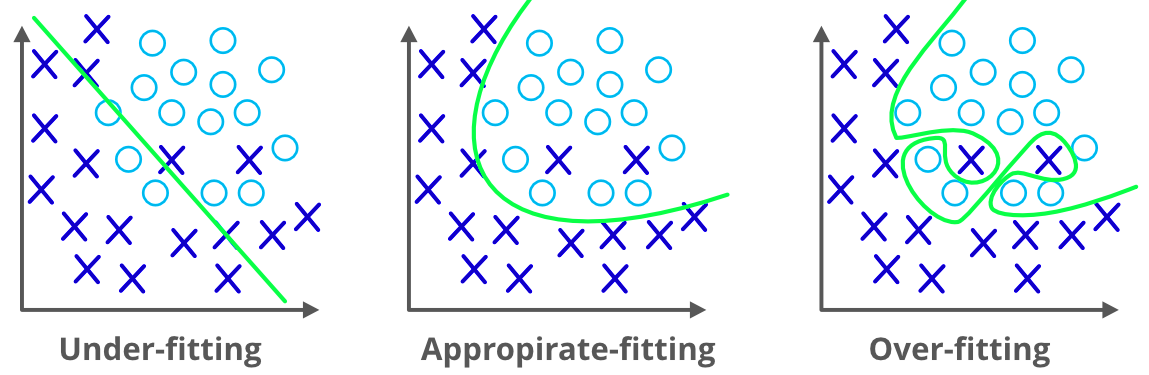
在继续之前，我们需要了解什么是过拟合问题。当一个机器学习模型在训练数据集上表现良好，但在使用测试数据集时却失败或产生错误时，就会发生过拟合。我们无法使用该模型来预测实值输入变量的输出。为了处理这个问题，我们可以使用正则化。

正则化方法是如何起作用的？

在正则化方法中，我们使用模型中的所有特征，但我们要做的是减小特征的量级，使其成为一个更准确、更泛化的模型以给出好的结果。换句话说，正则化减少了对更复杂模型的使用，从而降低了过拟合的风险。
 

正则化方法通过添加额外的约束来做两件事：

1.     解决一个不适定问题（一个没有唯一且稳定解的问题）
2.     防止模型过拟合

在机器学习中，正则化问题对成本函数施加了一个额外的惩罚。这个惩罚控制了模型的复杂性——惩罚越大，模型越简单。这使得模型不会对数据过拟合，并遵循奥卡姆剃刀原则：简单的模型通常是更正确的模型。

正则化问题的一般形式如下所示

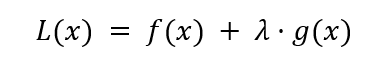
其中 f(x) 是一个损失函数（如残差平方和），λ 是控制模型复杂度的正则化项，而 g(x) 是另一个作为回归系数函数的函数。

不同的 g(x) 函数本质上是不同的机器学习算法。

正则化技术

我们已经讨论了正则化中使用的两种主要技术，它们是

1. L2 正则化或岭回归
2. L1 正则化或 Lasso 回归
3. Dropout 正则化

岭回归

岭回归是一种灵活而强大的回归分析，当输入变量之间存在高度相关性时使用。如果共线性非常高，我们会在岭回归方法中加入一些偏置。我们加入的偏置量在岭回归中被称为惩罚。岭回归对过拟合问题的敏感性较低。

岭回归有助于解决参数数量众多且它们之间高度相关的问题。岭回归也用于降低模型的复杂度，我们称之为 L2 正则化。

岭回归是正则化的一种形式，它减少了数据集中相关特征的影响。它通过惩罚较大的系数，缩小非信息性特定特征的系数来实现这一点。
 

基础与解释

岭回归的数学公式如下所示

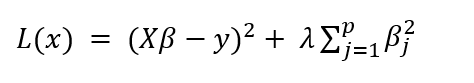
左边项是残差平方和——衡量模型误差与实际值的度量。右边项是惩罚项。注意，惩罚是 β^2 的函数，它作为线性模型的约束。

岭回归的关键点在于，模型倾向于选择接近 0 的较小的 β 估计值，这会减少惩罚项。

关于调整正则化参数 λ 的说明

正则化项 λ 对模型性能有深远影响，应谨慎选择。一种方法是简单地观察 λ 的不同值如何影响模型性能。

我们将编写一种使用交叉验证的方法来实现这一点，这是一种评估模型的重要策略，超出了本教程的范围。

模型训练

我们将使用线性回归教程中描述的波士顿数据来预测中位数房价。

首先，加载波士顿数据集。

# Import the dataset
from sklearn.datasets import load_boston

data = load_boston() 
print(data)

# Import general-use data science libraries
import pandas as pd
import numpy as np

# Import features
df = pd.DataFrame(data=data.data, 
                  columns=data.feature_names)
print(df)

# Import target (median housing prices)
target = pd.DataFrame(data=data.target, 
                      columns=["MEDV"])
print(target)
 

然后将其分为训练集和测试集。

from sklearn.model_selection import train_test_split
Xtrain, Xtest, Ytrain, Ytest = train_test_split(df, target, test_size=0.8, random_state=1)

print("Dataset sizes after train_test_split()")
print("Xtrain size: ", str(np.shape(Xtrain)))
print("Xtest size: ", str(np.shape(Xtest)))
print("Ytrain size: ", str(np.shape(Ytrain)))
print("Ytest size: ", str(np.shape(Ytest)))
 

通过超参数调优来拟合岭回归模型

# Fit the model
from sklearn.linear_model import RidgeCV
import numpy as np
lambdas = np.array([1.e-06, 1.e-05, 1.e-04, 1.e-03, 1.e-02, 1.e-01, 1.e+00, 1.e+01,
      1.e+02, 1.e+03, 1.e+04, 1.e+05, 1.e+06])
ridge_mdl = RidgeCV(alphas=lambdas).fit(Xtrain, Ytrain)
 

Lasso 回归

与岭回归一样，Lasso 回归也通过添加一些惩罚来降低模型的复杂性。唯一的区别是，在 Lasso 中，我们将实际值作为惩罚，而在岭回归中，我们使用的是该值的平方。

最小绝对值收缩和选择算子 (LASSO) 是另一种形式的正则化。它允许回归系数一直收缩到 0。这使得模型更稀疏且计算效率更高。Lasso 回归也称为 L1 正则化。

此外，LASSO 会执行特征选择：系数为 0 的特征基本上被忽略了。
 

基础与解释

LASSO 的数学公式如下所示

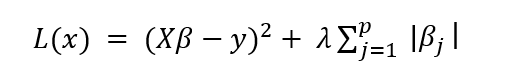
与岭回归公式唯一改变的是惩罚项中的绝对值。

通过几何视角理解岭回归和 LASSO

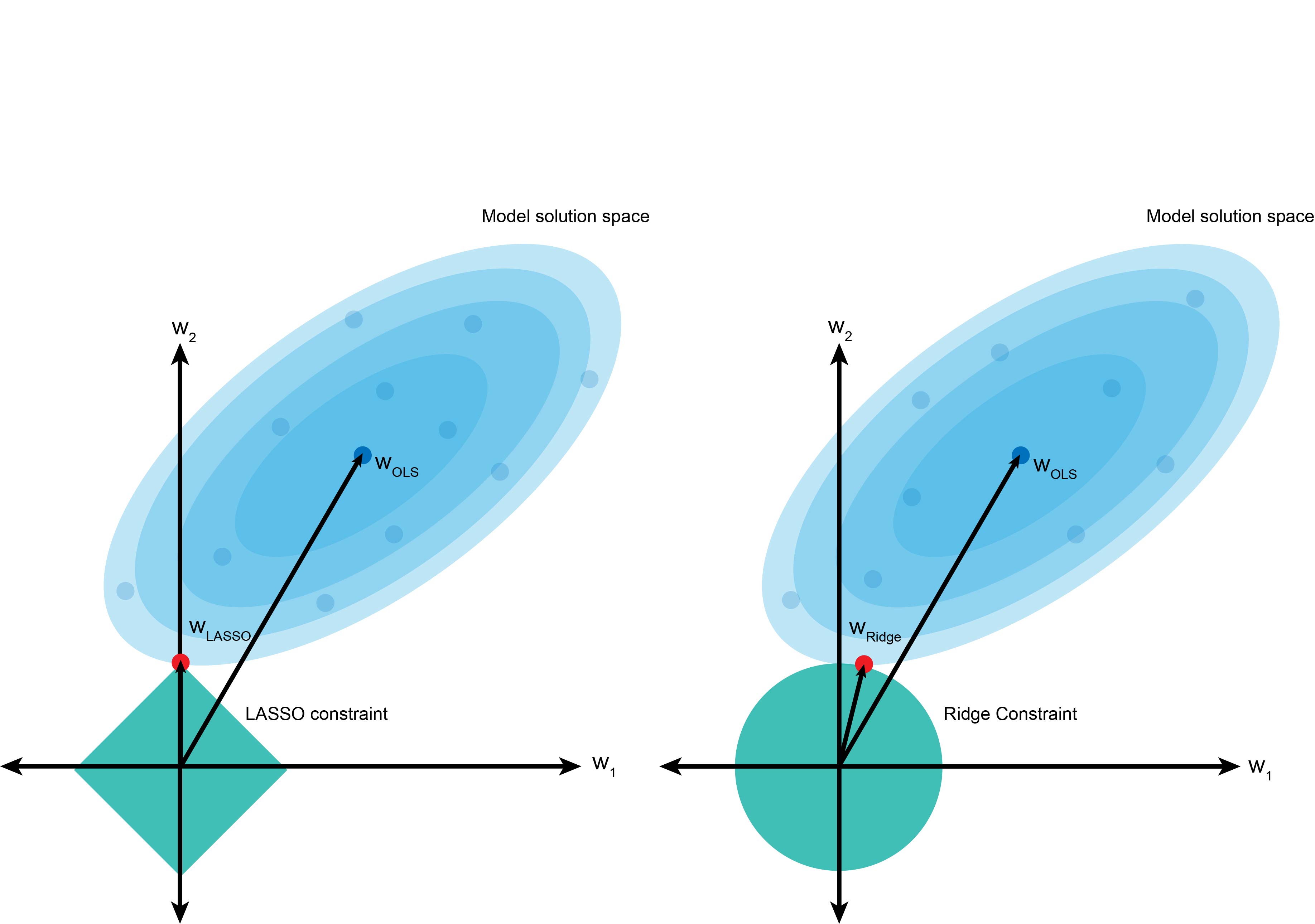
上图是 LASSO（左）和岭回归（右）的视觉表示。蓝色云代表最小二乘运算，中心值是 β 的最小二乘估计值。

然而，惩罚项迫使我们不取那个值，而是在绿松石色边界内选择值。如果我们考虑一个二维问题 (β₁²+β₂²)，岭回归中的平方项会产生一个圆形。相比之下，LASSO 中的绝对值项创建了一个菱形约束。

使用相同的最小二乘模型，岭回归中的圆形约束使得系数 w₂ 很可能被收缩为一个接近 0 的小值（如红色所示），但不一定会达到 0。相比之下，如果系数 w₂ 不具信息性，LASSO 更可能对其进行更严厉的惩罚并将其设置为 0。

模型训练

正如我们对线性回归和岭回归模型所做的那样，我们将在波士顿数据集上使用超参数调优来训练 LASSO。

# Fit the model
from sklearn.linear_model import LassoCV
import numpy as np
lambdas = np.array([1.e-06, 1.e-05, 1.e-04, 1.e-03, 1.e-02, 1.e-01, 1.e+00, 1.e+01,
      1.e+02, 1.e+03, 1.e+04, 1.e+05, 1.e+06])
lasso_mdl = LassoCV(alphas=lambdas).fit(Xtrain, Ytrain)