朴素贝叶斯

朴素贝叶斯是一种监督机器学习算法，用于解决分类问题。朴素贝叶斯主要用于测试分类问题，它基于贝叶斯定理的原理工作。

众所周知，监督机器学习使用训练数据集来训练模型，在这种方法中，它使用高维训练集。朴素贝叶斯算法简单、非常准确，并提高了模型的效率，使得模型在给出预测时非常快。

朴素贝叶斯算法基于概率工作，它被称为概率分类器算法。朴素贝叶斯算法的流行示例包括文章分类器和垃圾邮件检测与过滤。

贝叶斯定理

与假设世界随机运作的传统统计方法相比，贝叶斯统计旨在利用过去事件或经验的知识来模拟事件发生的概率。

贝叶斯定理的核心思想是，我们试图在不知道数据与类别之间因果关系的情况下，根据数据估计给定类别之间的关系（或概率）。

在数学上，这可以用以下公式表示，我们将在后续部分详细解释这些点

后验概率（或预测）：P(类别 | 数据)

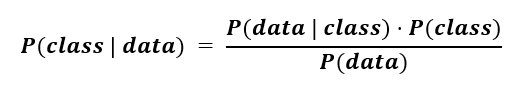
P(类别 | 数据)是类别与给定数据集关联的概率。这被称为条件概率或后验概率。

这是我们在分类问题中旨在估计的正式定义：我们正在尝试预测给定一些数据属性，数据点属于特定类别的几率。

先验信息：P(类别)

现在，数据集中给定类别出现的概率 P(类别)相对容易估计——我们可以看到类别出现的频率。这个术语被称为先验，因为它来源于对数据的先验知识。

似然：P(数据 | 类别)

此外，数据点与给定类别关联的概率（P(数据 | 类别)）也容易获得。在这种情况下，我们可能碰巧知道重要特征的某些阈值，这些阈值会增加数据点被归类到某个类别的几率。这被称为似然。

证据：P(数据)

最后，我们可能（或可能不）拥有有关数据中给定特征分布的信息。这通常需要通过大量的先前示例来估计，因为这将提供证据表明我们的数据具有特定形式。尽管如此，我们可以对数据进行假设，使这个变量可以忽略不计。

综合起来

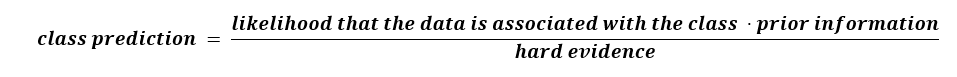
现在，如果我们重新审视这个公式，我们可以用一些能传达数学直觉的词语来重新阐述贝叶斯定理

虽然在实践中很难使用贝叶斯定理（因为我们通常没有确凿的证据），但我们可以做出一些假设，从而建立预测模型。其中一种简化就是朴素贝叶斯。

为什么它被称为朴素贝叶斯算法？

那么，为什么这种机器学习算法被称为朴素贝叶斯呢？我们知道这个算法是基于贝叶斯定理的，这就是它被称为贝叶斯的原因。而“朴素”的意思是特征之间相互独立。

假设我们有一个橙子，它具有颜色和形状等特征，这些特征各自独立地对特征做出贡献，并且互不依赖。

朴素贝叶斯

朴素贝叶斯使用贝叶斯定理，但为了简化数学，它做了1个（朴素的）假设：训练数据集中的所有特征都被认为是相互无关的。

换句话说，每个特征都是相互独立的，特征之间没有相关性（或反相关性）。

为什么这很重要？由于我们不知道底层数据分布，并且我们选择不承认它，我们可以忽略分母。因此，计算简化为一个加法公式，我们将每个 p 特征对观察给定类别 k 的可能性进行求和

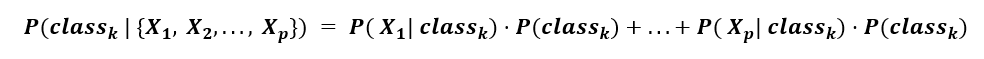
注意：这意味着数据中的每个特征都与给定类别具有某种预测关系，并且这种关系被假定独立于数据中的其他特征。虽然这在所有真实世界数据集中并不成立，但这种方法却出奇地有效，并具有很高的准确性！

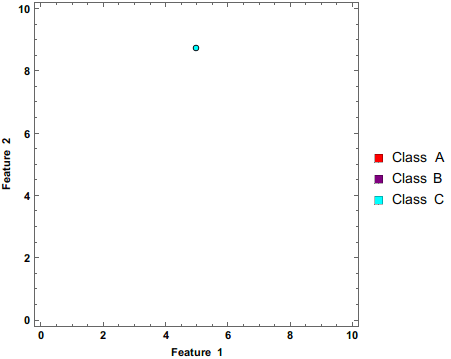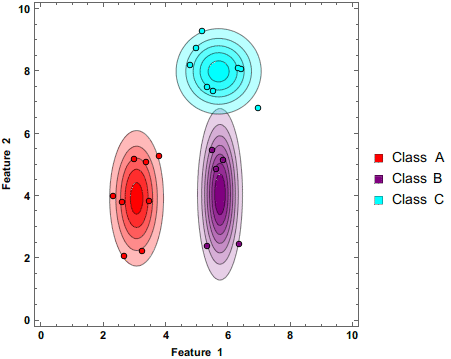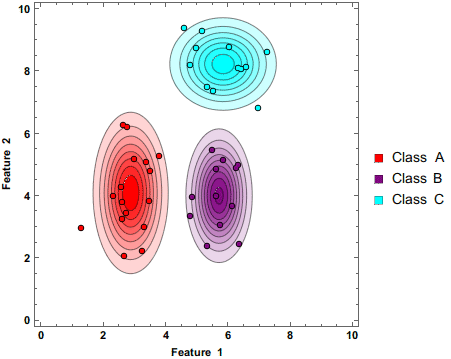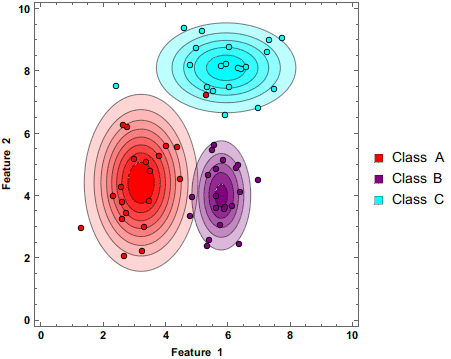
上图显示了朴素贝叶斯分类器在添加额外数据点时将3个类别分离。请注意，圆圈的颜色较深。这表明这些预测是基于概率做出的。

朴素贝叶斯算法的工作原理

我们可以通过一个简单的例子来检查朴素贝叶斯算法的工作原理，这使得理解起来更容易。假设我们有一些关于天气的数据，我们需要预测在特定的一天是否可以外出，这取决于天气条件。为此，我们必须执行一些步骤以进行适当的预测
1.    我们将给定的数据集转换为频率表
2.    使用天气数据生成一个雨天概率表
3.    使用贝叶斯定理预测输出

现在我们有一个问题：如果天气晴朗，我们可以出去吗？

为了得到解决方案，我们必须检查下表

现在我们有一个基于天气条件频率的表格

那么天气的似然表将是

准备好表格后，我们必须应用贝叶斯定理进行预测。

P(是|晴天) = P(晴天|是)*P(是)/P(晴天)
P(晴天|是)= 3/10 = 0.3
P(晴天)= 0.35
P(是)=0.71
所以 P(是|晴天) = 0.3*0.71/0.35 = 0.60

P(否|晴天) = P(晴天|否)*P(否)/P(晴天)
P(晴天|否)= 2/4=0.5
P(否)= 0.29
P(晴天)= 0.35
所以 P(否|晴天)= 0.5*0.29/0.35 = 0.41

从以上计算中得出 P(是|晴天) > P(否|晴天)
这意味着我们预测我们可以在晴天外出。

朴素贝叶斯的优点

• 正如我们所说，它是一个简单快速的机器学习算法
• 它适用于二分类和多分类
• 在多类别数据集的情况下，它将做出良好而准确的预测。
• 它可以完美地用于文本分类

朴素贝叶斯的局限性

• 在“为什么叫朴素贝叶斯”一节中，我们提到它认为所有特征都是独立的，因此它无法发现特征之间的关系。

朴素贝叶斯的应用

• 有助于实时预测
• 可用于垃圾邮件过滤
• 用于医疗领域
• 有助于信用评分

朴素贝叶斯模型的类型

朴素贝叶斯算法分为三种类型：

1. 高斯：这是一种模型假设特征服从正态分布的方法。这意味着如果输出取连续值，模型会认为它是高斯分布。
2. 多项式：如果数据服从多项式分布，我们将使用多项式朴素贝叶斯模型，它主要用于文本分类。
3. 伯努利：伯努利分类器与多项式分类器相似，但区别在于输出变量是独立的二元变量。它用于检测文档中是否存在某个词。