


逻辑回归是最简单和最基本的机器学习算法之一,属于监督学习分类算法,它通过使用一组输入或独立变量来帮助确定预测变量的类别。
我们可以说,当预测值本质上是二元的时,即预测变量只属于“是”或“否”或“0”或“1”这两个类别中的任何一个时,就使用逻辑回归。但在某些情况下,它会给出一个介于0和1之间的概率值。
逻辑回归用于预测概率,这与回归算法中的线性回归非常相似。主要的区别在于它们的用途,逻辑回归用于分类问题,而线性回归用于回归类型问题。
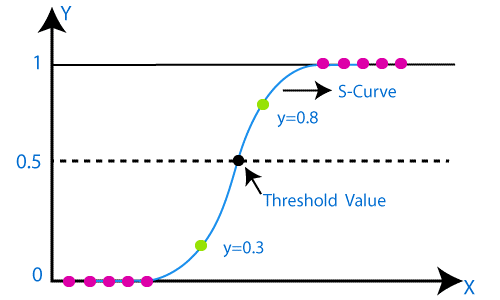
与线性回归的图是一条直线不同,逻辑回归的图倾向于在0和1之间呈现“S”形。从逻辑函数中的这条曲线,我们可以理解它是否是垃圾邮件,或者是否是欺诈。
根据类别数量和预测变量,我们可以将逻辑回归分为三种类型。通常,如上所述,逻辑回归具有二元值,但内部有3种类型。
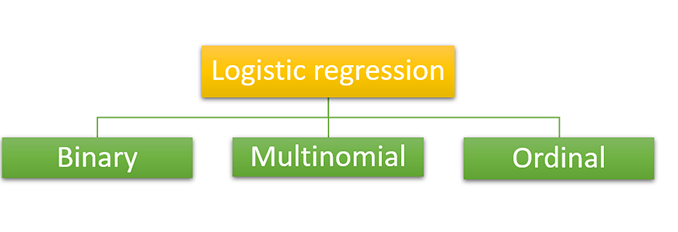
如我们所知,在二元分类中,预测变量只有两种可能性,要么是零,要么是一。它将类似于“是”或“否”条件,可用于检测是否是垃圾邮件。
在多项式分类中,预测变量可能具有三个或更多结果的概率,例如类型 A、类型 B 或类型 C 等,并且类别之间没有关系或依赖性。它用于创建不同的类别,如形状、颜色或水果等。
它也是一种多项式分类,预测变量可能具有三个或更多结果,但结果的类别将是有序的,这意味着它们具有很强的关系或依赖性。例如,考虑学生的成绩类别,如“好”、“非常好”和“优秀”。这三者都相互具有定量意义。
为了逻辑回归的顺利运行,我们有两个重要的假设,否则可能会导致不准确或错误的结果。它们是
如我们在之前的回归主题中学到的,逻辑回归的实现也使用相同的步骤,即
到目前为止,您可能想知道我们是否可以将线性回归用于分类任务。毕竟,一种构建分类任务的方法是确定分隔不同类别的最佳直线。
然而,线性回归明确地尝试识别描述数据之间关系的趋势,而不是最佳的类别分隔符。因此,由于以下原因,线性回归不是合适的分类方法
逻辑回归通过尝试计算数据点属于给定类别的概率来解决这个问题。它是一种解决二元分类问题的有用模型。
假设我们有 80% 的把握 (p=0.8) 一个给定的数据点属于类别 A。我们成功的几率是 p/(1-p)=0.8/(1-0.8)=4。这意味着我们成功的几率为 4:1,几率越高,给定结果的可能性就越大。
然而,理论上,几率可以取 0 到 ∞ 之间的任何数字。这使得为给定数据点分类制定规则变得非常困难。因此,我们需要一个更好的度量来进行分类,一个直观的度量是使用概率。
为了用概率表示线性方程,我们需要执行 logit 或 sigmoid 函数。我们取方程左侧的对数,我们假设它是成功的几率。
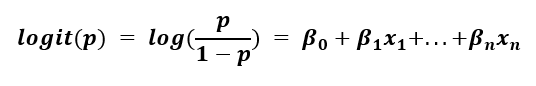
左侧被称为对数几率,其范围为 -∞ 到 ∞。这本质上是概率方面的线性回归问题:模型的输出可以是任何值,这对于分类问题没有用处。
然而,在逻辑回归中,我们求解数据点属于给定类别的概率。如果我们进行代数运算,我们得到以下表达式
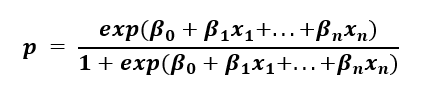
这种形式确保 p 在 0 到 1 的范围内,这正是二元分类任务所需的。
为了解释模型结果,如果数据属于类别 A 的概率小于 50%,这相当于随机分配 (p<0.5),那么我们可以说该数据点应归类为类别 B。
让我们比较一下给定相同数据的线性回归和逻辑回归。类别 A 的 P = 0,而类别 B 的 P = 1,并将其绘制为 x 的函数。
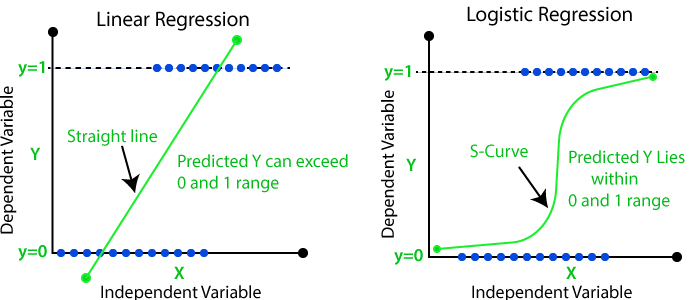
由于这两个原因,我们可以肯定地说,线性回归器不是对数据进行两类分类并用直线分隔数据的合适方法。相比之下,逻辑回归曲线完美地做到了这一点。此外,它具有高度可解释性:该线可视化了给定数据点属于某个类别的概率作为 x 的函数。
虽然逻辑回归是执行二元分类的一种有价值且直接的算法,但我们在线性回归中必须做出的相同假设在逻辑回归中仍然适用。