


现在我们已经了解了监督学习方法以及在监督学习中使用的不同回归和分类算法。现在是时候进一步学习非监督学习了,我们称之为无监督学习。
简单来说,无监督学习有助于解决更多实际问题,因为它类似于人脑,必须从数据集中学习底层模式,而无需构建完善的训练数据集。

无监督学习是另一种机器学习类型。目标是在没有人类干预的情况下,学习数据中潜在的模式和结构,而无需将其映射到响应变量或标签。相反,数据可以进行排序、压缩、聚类或可视化,从而使用户能够高层次地了解整个数据集。
换句话说,我们可以将无监督学习定义为在没有监督的情况下进行的学习。这意味着我们只有一个数据集,并且没有用于训练模型的给定训练数据集。因此,模型必须找到隐藏在数据集内部的内部模式和关系,并根据相似性对它们进行分类。
为了更清晰地理解,我们可以举一个蔬菜和水果的例子。无监督机器学习算法必须对蔬菜和水果的图片进行分类。不同之处在于,在监督学习中,有一个经过训练的数据集可以了解蔬菜和水果的特征以对其进行分类。在这里,算法对蔬菜或水果的特征一无所知;它必须自己识别图像中的相似性,并必须将给定数据集分类为水果和蔬菜。
无监督学习通过根据它从分析数据集中获得的相似性将图像聚类成组来完成这项工作。
数据探索
有时,我们得到一个数据集,但我们不知道要执行哪种分析。相反,我们被要求寻找数据中有趣的属性。
这就是无监督学习的用武之地——了解数据结构本身,没有任何强加的偏见。例如,通过对数据进行聚类,我们可以看到是否存在可以进一步分析的自然出现的模式。
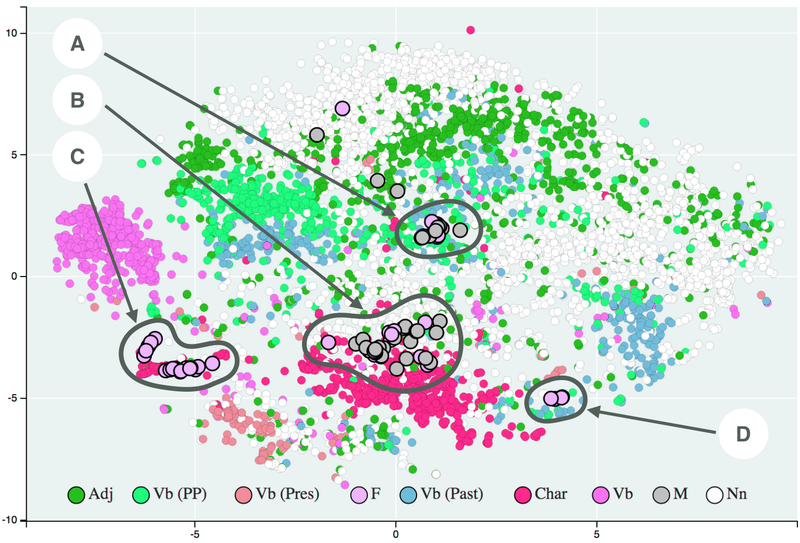
对于包含许多特征的数据集,如果没有一种方法来可视化这些高维数据集中的数据,就很难提取洞察力。
一些现代的无监督学习算法,如 T-SNE 和 UMAP,可以将高维数据集压缩成一个较小的集合。这些方法使数据可视化变得更容易,同时为底层数据结构提供了重要的见解。
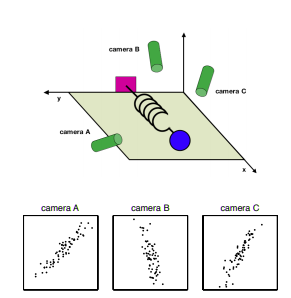
让我们以观察弹簧振荡来测量弹簧常数为例——一个经典的物理问题。我们提供三个摄像头,它们正在计算弹簧上球体的轨迹。
一个问题是,“我们是否在最佳方向上查看数据以测量我们的弹簧常数?”(答案是否定的)。这类似于训练机器学习模型,我们需要以最佳方式构建数据,以便模型可以提取尽可能多的信息。主成分分析等无监督方法可以通过去除数据中的相关性来做到这一点。
如果我们考虑上面的相机示例,我们注意到三个相机都在测量相同的事件,只是以略微不同的方式观察弹簧。因此,其中一些特征有点冗余。
无监督学习方法可以告诉我们哪些特征没有太多信息,或者彼此高度相关,从而使模型能够更有效地学习。
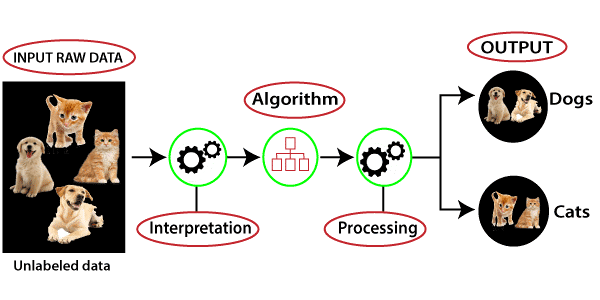
在这张图中,我们可以理解有一些原始数据,其中包含许多未排序和未分类的项目,这些项目被输入到机器学习算法中。它没有任何训练数据集或输出可以帮助排序数据,就像在监督学习中那样。
首先,机器学习算法会自行解释给定的数据集,以理解数据集中隐藏的模式,然后利用这些模式对数据集进行排序。
有许多算法可以与无监督算法一起使用。当我们应用合适的算法,如 k 均值聚类或决策树等时,它会根据从数据集中找到的模式将数据分组到不同的类别中。
聚类方法旨在根据相似性或与其他数据在同一集合中的差异对数据进行分组。我们已经在分类的背景下看到了 K-均值聚类的例子,其中数据点是根据质心进行分组的。还有许多其他方法可以对数据进行分组,例如层次聚类和 DBSCAN。
关联规则是一种帮助在大数据集中查找变量之间关系的方法。它有助于查找数据集中组合出现的那些数据集合。

你可以想象你在一家杂货店里,你正在寻找牛奶。根据经验,你知道牛奶在冷藏区,而没有人明确告诉你。此外,因为你要买牛奶,所以你很有可能在商店里买一些搭配牛奶的东西,比如麦片。
这种购买体验就是关联规则的一个例子,其目的是根据概率在给定数据集中找到变量之间的关系。
降维旨在减少数据集中特征的数量并对其进行压缩,以便只保留最有意义的特征。主成分分析是减少数据集中特征数量的一种方法。
使用无监督学习时,我们有一些优点,如下所示:
虽然无监督学习是建模和理解数据的好方法,但也有一些挑战需要注意