


现在我们将介绍机器学习算法的一个重要系列,它们在从搜索引擎到患者诊断的许多实际用例中都发挥着作用:聚类。因此,我们需要讨论聚类和聚类的类型。
机器学习专家的目标是建立一个能够提供准确预测的模型。我们已经讨论过,这些算法通常分为两种类型:
1. 监督式机器学习
2. 非监督式机器学习
K 均值聚类属于一种无监督学习算法,这意味着没有带标签的数据来训练模型。
聚类旨在将不同的数据点分组到彼此相似的集合中,并与其他组区分开来。在聚类的背景下,相似性由坐标系中两个数据点之间的距离定义。如果我们对为特定数据点分配标签感兴趣,这是一个分类问题。然而,聚类也可以是一个无监督学习问题,具体取决于应用。
各种聚类类型有
1. 层次聚类:在层次聚类中,它使用树状结构进行聚类。
2. 划分聚类:在划分聚类中,数据点被划分为不同的分区。
层次聚类又可以进一步分为
1. 凝聚聚类
2. 分裂聚类
划分聚类分为
1. K 均值聚类
2. 模糊 C 均值聚类
有几种算法以不同的方式对数据进行聚类,但我们将重点关注一种简单且广泛使用的算法:K 均值聚类。
K 均值聚类是一种旨在将数据点分为 k 个簇的方法。请注意,参数 k 是用户定义的——我们需要告诉算法数据中有多少组。
例如,如果 k = 2,这意味着将只有 2 个簇。如果 k = 3,这意味着将有 3 个簇。
使用 K 均值算法,我们可以将数据聚类成不同的组或类别。它帮助我们理解这些类别,并将未标记的数据分类到这些类别中,而无需使用训练数据集或训练模型。
K 均值聚类基于质心,这意味着在 K 均值算法中,每个簇都有一个质心,算法尝试减少数据与其数据簇之间的距离之和。
在此算法中,它接收未标记的数据,并使用参数 K 将这些数据分成用户指定的簇数。此过程重复进行,直到获得完美的簇。
K 均值算法有三个通用步骤
之后,我们将得到具有共同特征的数据点的簇。下面是 K 均值聚类在实际应用中的表示。黑色的“+”号是最初随机分配的质心。黑线表示决策边界:算法学习到的将数据点分隔到不同簇的规则。
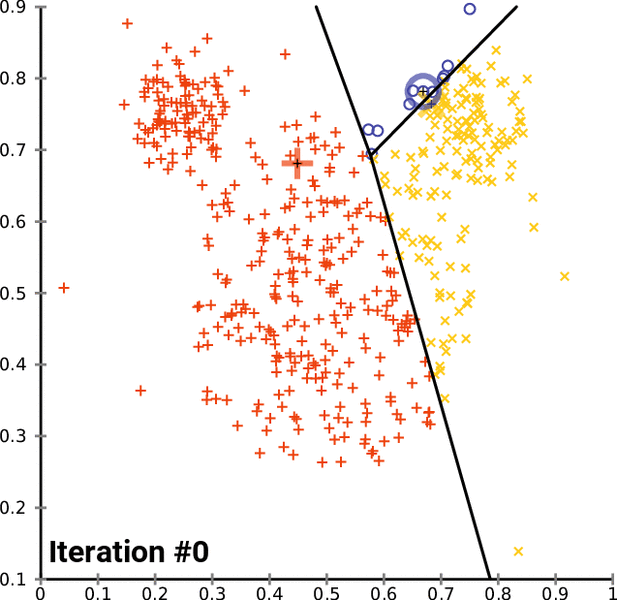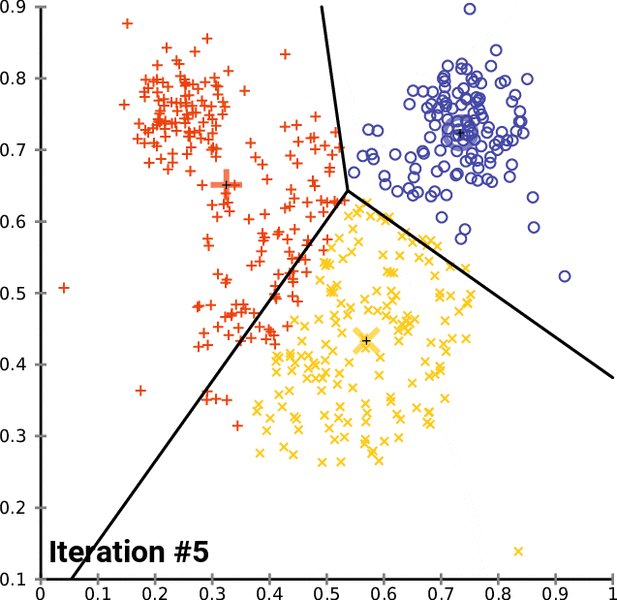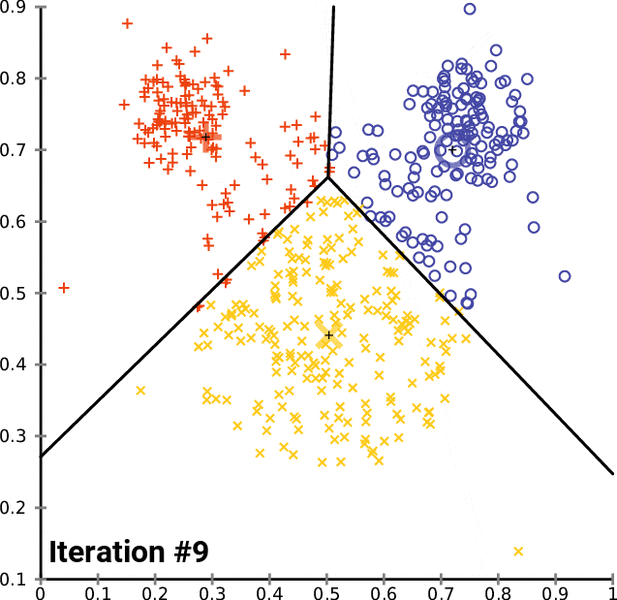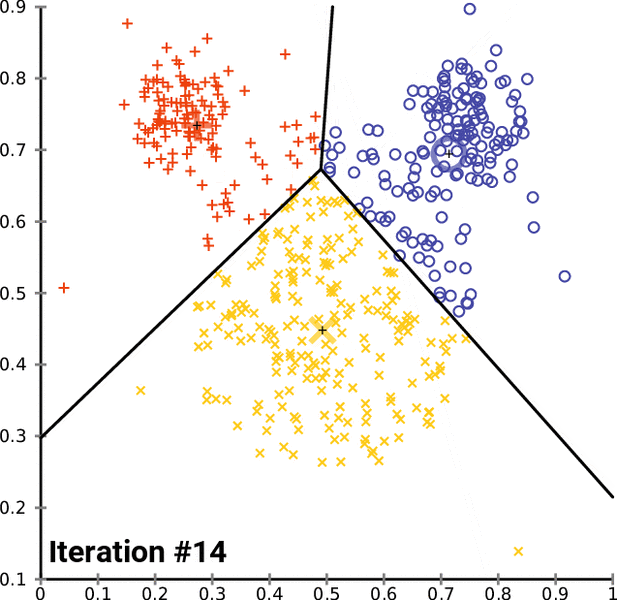
对于每次迭代,我们都在计算每个数据点和质心之间的距离。每次迭代后,对不同类别的分配都会改变。新的簇分配会改变质心位置,因为我们正在确定给定簇的新中心值。
每次迭代后,随着算法随着时间的推移找到类之间的最佳分离,类分配趋于稳定。这种模型分配的稳定化被称为模型收敛。
现在我们对 K 均值聚类及其工作原理有了基本的了解,现在我们将详细了解 K 均值聚类的工作原理。
步骤 1:使用参数 K 决定所需的簇数量
步骤 2:选择质心或一些随机点 [不需要来自数据集]
步骤 3:将数据点添加到最近的质心,这些质心将来自簇。
步骤 4:计算方差并为每个簇创建与方差相关的质心
步骤 5:将数据点重新分配到新的质心并创建新的簇
步骤 6:如果发生任何重新分配,请从步骤 4 重复
步骤 7:完成模型并准备投入使用。
K 均值聚类工作原理的详细视图
假设我们有两个数据变量 s1 和 s2。这些数据变量的图形表示如下所示。

现在我们要决定参数K的值,这意味着我们必须决定有多少个簇,这里我们提供k=2。现在我们需要将这些数据点分组到这两个簇中。寻找K值有多种方法可用。
下一步是确定质心,目前我们只是将一些随机的 k 个点作为质心来创建簇。这些随机点可能来自数据集,也可能来自任何外部点。在下图中,我们选择了与数据集不同的质心。

下一步是将这些图中的数据点分配给质心或 k 点。我们使用计算点之间距离的相同公式。之后,我们必须在两个质心之间画一条线,称为中位数。

现在我们有了中位数,从图中可以看出,中位数上方的点靠近绿色质心,中位数下方的点靠近黄色质心。因此,我们根据质心将数据点的颜色更改为绿色和蓝色,如下图所示。

现在我们有一些点属于两个质心。现在我们必须找到最近的簇,以便我们重复这个过程并找到一个新的质心,它几乎是质心的中心,如图所示。
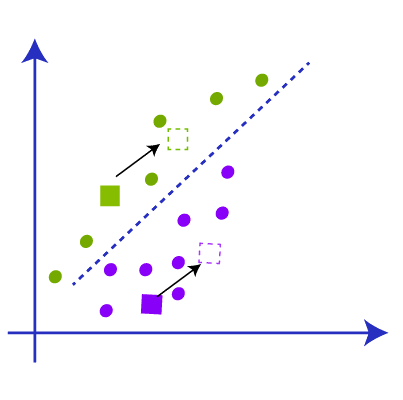
现在我们得到了新的质心,我们重复将数据点链接到新质心的过程,并根据新质心绘制新的中位数,如下图所示。

现在当我们检查上面的图片时,我们可以发现一个黄色数据点低于新的中位数,两个绿色数据点高于中位数。因此,我们必须将这些数据点链接到各自的新质心,如下图所示。

因此,在与新数据点重新链接质心之后,簇的重心会发生变化,我们必须重复该步骤以找到具有新数据点的新质心。如下图所示。

再次,我们必须找到新簇的新中位数,并在质心之间绘制中位数,如下图所示。我们现在正在重复上述步骤。
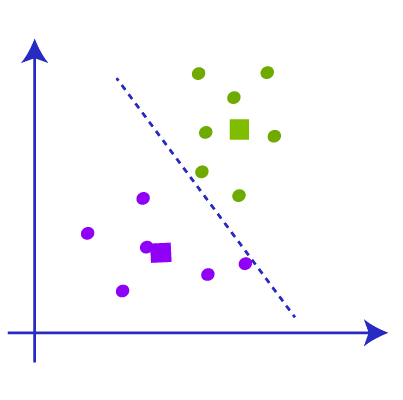
现在当我们检查数据点时,将没有任何点需要重新分配,因此聚类完成,我们的模型也几乎完成
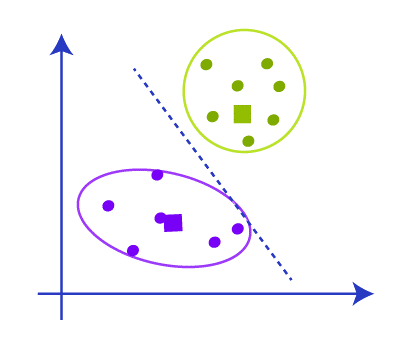
形成簇后,我们必须移除质心、中位数以及我们为创建簇而构建的所有其他结构,最终的簇将是

K 均值聚类完全依赖于簇,并且在确定将影响模型准确性的最佳簇数量方面非常重要。有许多方法可以找到 k 值,其中最重要的是:
这是一种流行且常见的方法来找到最佳的 k 值。这种方法使用 WCSS 的概念,即“簇内平方和”,它使用公式来找到 k 值。
这用于计算 3 个簇的 WCSS 值。
K 均值聚类是一种无监督机器学习方法,它在现实世界中具有广泛的适用性,其中一些是:
K 均值聚类是一种强大且直观的数据分组方法。然而,我们对 K 均值聚类的数据做出了几个假设
簇的大小需要相同。
在上面的例子中,黄色比蓝色和红色大得多,导致了一些错误分类。
数据方差或数据点的分布需要相同。
同样,黄色的分布或方差比蓝色和红色更分散,导致了一些错误分类。
最后,K 均值更适用于“球形”数据集关系。
这在技术上意味着方差需要大致相同。
最后,虽然我们可以使用实际类别数量来指定超参数 k,但我们通常不知道数据中的类别数量。在这些情况下,在无监督问题中确定 k 参数可能具有挑战性。