判别分析

我们发现逻辑回归是一种用于二分类的有用算法，它通过映射类的对数几率与数据之间的线性关系来实现。然而，逻辑回归仍然受限于线性假设。

在本教程中，我们将讨论**判别函数**：试图识别哪些变量组合可以分离多个类的函数。

逻辑回归的局限性或线性判别分析的需求

逻辑回归是一种强大而有效的分类算法，属于监督学习。但它有一些局限性，导致了LDA和其他算法的形成。

1. **二元问题**：正如我们所知，逻辑回归在二分类问题中非常有效。它也有多分类功能，但使用不多。
2. **不稳定**：逻辑回归在正常情况下表现完美，但当类别完美分离时，逻辑回归会变得不稳定。
3. **数据量少时表现不佳**：如果数据不足以估计参数，逻辑回归可能会导致一些错误，我们称其为不稳定。

LDA解决了这些问题，并且在存在这些条件中的任何一种时，可以代替逻辑回归使用。如果尝试两种方法并选择最佳方法，那将是很好的。

线性判别分析

**线性判别分析（LDA）**是一种降维方法，常用于监督机器学习中的分类问题。它用于投影类别的差异。简单来说，我们可以说它用于将高维空间中组的特征显示到低维空间。

假设我们有两组具有不同特征的不同数据，我们想用一个特征将它们分开或分类。当我们这样做时，可能会有很高的重叠机会，如图所示。因此，我们必须增加特征的数量才能进行良好的分类。
 

考虑一个例子来使概念更清晰。让我们有两组不同组的数据。现在我们想将它们分成两个不同的组，就像2D图片中那样。但是当我们尝试在2D图中绘制数据点时，将没有线性线来将数据分成两组。

在这种情况下，我们使用线性判别分析将2D图降维到一维图，从而在两组数据点之间获得更大的可分离性。

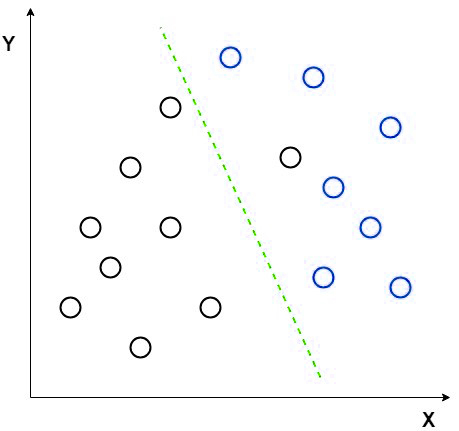
在这种方法中，LDA使用图坐标（如X轴和Y轴）创建一个新坐标，并使用新坐标或轴显示数据。因此，我们实现了2D图的一维降维，并有助于增加分离。

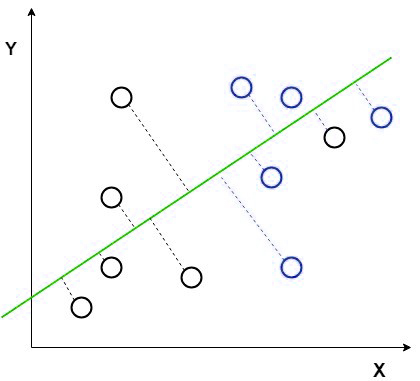
新的坐标由两条规则组成：

• 将两组均值之间的距离最大化。
• 将两组方差最小化。

在上面的图片中，我们用红色显示了新轴，并根据新轴绘制了数据点，使得两组均值之间的距离增加，两组之间的方差减小。

根据我们的规则在新轴上绘制数据点后，它将如下图所示。

上面的函数是判别函数，它告诉我们一个数据点属于类**k**的可能性。请注意，**π_k**是类k的先验，f_k是类**k**数据的概率密度函数。

对于LDA，我们将假设数据服从均值为**μ_k**的正态分布。我们还将假设协方差矩阵**Σ**在所有类中都是相同的。因此，我们得到以下判别函数
 

关键点是：**如果我们比较任意两个类别，最能将这两个类别分开的线是线性函数**。因此，LDA找到最佳的线来分离任意两个类别。

我们无法一直使用这种线性判别分析，因为如果均值共享，LDA将无法找到新的坐标和轴，它将失败。在这种情况下，我们使用非线性判别。非线性判别的一些流行例子是：

1. **二次判别分析**：在此方法中，每个类都有自己的方差估计。如果有两个以上的输入，则为协方差。
2. **灵活判别分析**：它将用于我们在之前的教程中讨论的样条，因为输入是非线性组合。
3. **正则化判别分析**：我们知道什么是正则化，在这种方法中，我们在方差估计中引入正则化。这有助于减少变量对LDA的影响。

二次判别分析

现在，如果我们想找到可以分离更多非线性数据的曲线怎么办？要完成这项更复杂的任务，我们需要确定并考虑每个类的方差差异。

二次判别分析优于线性判别分析的一个例子。

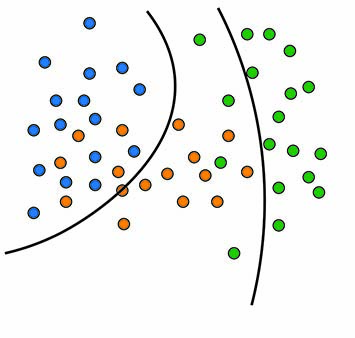
如果我们不假设每个类的方差相同，则判别函数会变得更加复杂。

关键在于，通过不假设方差相等，判别函数变为二次函数。这使我们能够分离方差不相等的非线性数据。

何时选择线性判别分析还是二次判别分析？

判别分析对于使用线性和非线性决策边界对数据进行分类很有用，但在特定情况下，您会希望使用一种算法而不是另一种算法。

下表描述了选择线性判别分析和二次判别分析的用例。