


在上一节中,我们回顾了几种扩展线性模型以减少过拟合的方法。然而,如果数据与输出之间的关系确实是非线性的,我们需要采用更复杂的模型。
在多项式回归中,我们可以借助 n次方变量在自变量和预测输出之间建立关系,这有助于展示比线性回归更复杂的关系。
多项式回归的方程如下所示:
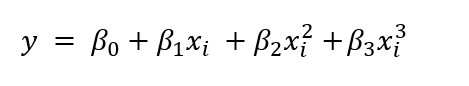
我们可以说多项式回归是线性回归的一个特例,因为我们通过在多元线性回归中添加 n次方多项式来构建多项式回归。简单来说,我们可以说多项式回归是经过一些修改以提高准确性的线性回归。
它使用经过一些修改的线性回归图来包含复杂的非线性函数。在这种情况下,我们使用的是非线性数据集。
多项式回归的重要性
正如我们所知,第一点是,我们不能对非线性数据集使用线性回归方法。如果这样做,将会产生巨大的误差和非常低的准确性。对于此类非线性数据集,我们使用多项式回归,它可以通过最大数据点生成图表。
对于非线性数据集,数据点将以非线性方式排列,因此我们无法用一条直线连接数据点。通过图表我们可以清楚地理解这一点。
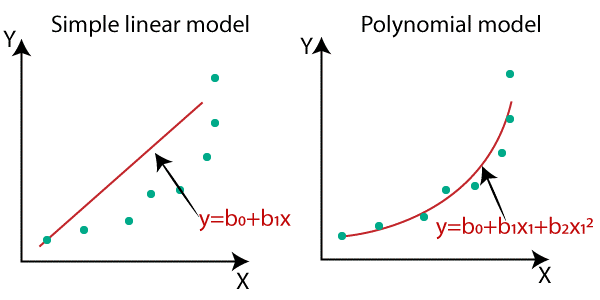
因此,从比较图中我们可以理解,如果数据集是非线性的,我们必须使用非线性图或多项式回归才能获得良好的准确性和更好的结果。
我们可以将它应用于输入数据集非线性的领域,这意味着在一些复杂的结果中,例如:
本教程将探讨我们如何利用多项式回归捕捉更多非线性趋势。
回顾线性回归教程可知,如果回归系数 β 和预测变量 x 彼此成比例,那么模型被认为是线性的,尽管数据集本身具有非线性变换。
下面的方程是一个线性回归问题,尽管它更复杂:
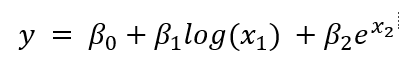
下面的方程是非线性的,因为它与预测变量不成比例。
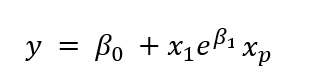
虽然我们可以使我们的模型像上面的方程一样更复杂,但我们将坚持使用通过更高阶多项式项使特征更复杂的案例。因此,模型仍然是线性的,因为关系可以由 β 进行缩放,并且每个特征的贡献是可加的。
让我们考虑一下波士顿数据集,其中包含与波士顿房价相关的数据。有一个名为 LSTAT 的变量,表示属于人口较低社会地位的个体百分比。
让我们可视化 LSTAT 与目标变量 MDEV(波士顿房价中位数)之间的关系。
import matplotlib.pyplot as plt
plt.figure(dpi=200)
plt.scatter(df["LSTAT"], target)
plt.xlabel("LSTAT")
plt.ylabel("MDEV")
plt.title("Relationship between LSTAT and MDEV")
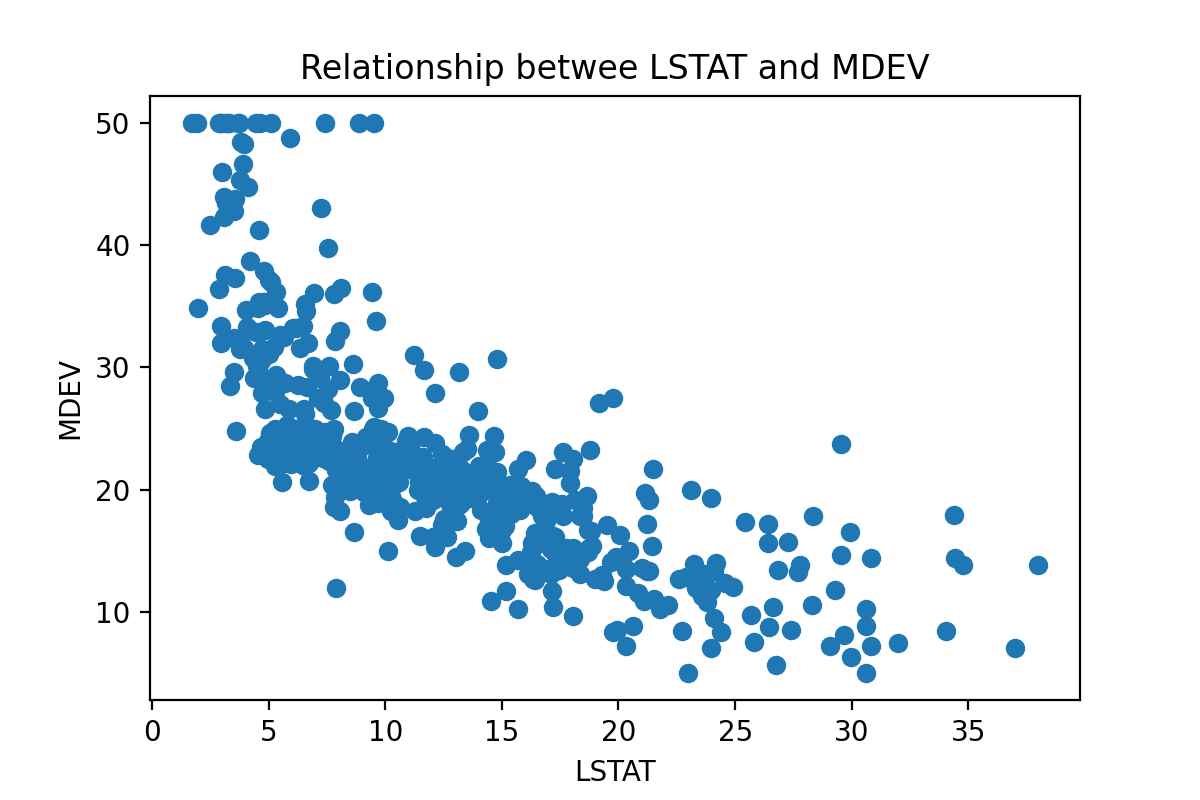
MDEV 和 LSTAT 之间的关系不是线性的。如果我们尝试用一条直线拟合这个数据集,我们将无法获得很好的结果,因为非线性数据会使直线偏斜。
让我们尝试通过这两个变量创建一个简单的多项式模型。具体来说,我们可以使用以下关系来构建模型:
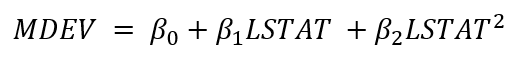
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression as lm
# Create the polynomial dataset with the squared term.
pol_model = PolynomialFeatures(degree=2)
lstat_pol = pol_model.fit_transform(pd.DataFrame(Xtrain["LSTAT"]))
# Fit a linear model
pol_model = lm().fit(lstat_pol, Ytrain)
# Plot it.
plt.figure(dpi=200)
plt.scatter(Xtrain["LSTAT"], Ytrain, color='red')
plt.scatter(pd.DataFrame(Xtrain["LSTAT"]),
pol_model.predict(lstat_pol),
color='blue')
plt.title("Polynomial regression prediction")
plt.xlabel('LSTAT')
plt.ylabel('MDEV')
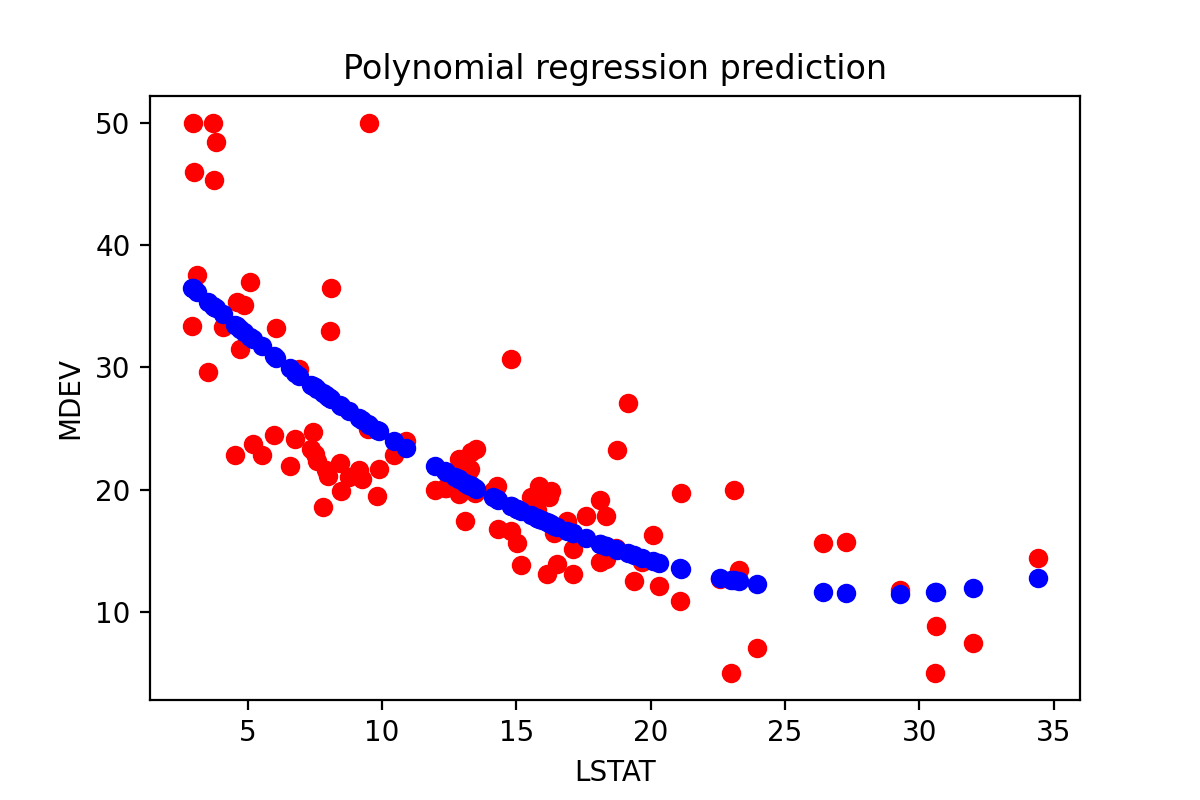
尽管我们选择了一个相对简单的多项式,但仅仅通过肉眼观察训练数据集(红色)和预测(蓝色)之间的关系,我们就可以发现模型比直线更好地拟合数据。
如果我们选择更复杂的模型,我们可能会获得更好的数据拟合。然而,随着我们不断添加更多多项式项,我们面临过拟合的风险。这是我们需要系统评估的问题,可以使用交叉验证或关于数据集分布的先验知识等方法。
不幸的是,多项式回归训练可能需要很长时间,这取决于问题的计算复杂度——换句话说,我们尝试拟合的方程的复杂性将影响计算时间。此外,随着模型变得更加复杂,它更容易过拟合。因此,多项式回归可以用于建模简单的非线性关系,但在实际情况中可能需要一些时间来微调和训练。