


回归分析是一种简单的方法,用于显示单个预测值(我们称之为目标)与多个预测值之间的某种关系。
在这里,目标变量依赖于输入的预测值,但输入值是独立的。如果目标值是连续值,例如薪水、年龄或体重,我们可以使用回归分析。此外,我们还在以下方面使用它:
为了更好地理解,让我们简化回归分析,它将向我们展示目标值是如何变化的,它依赖于输入值,以及在其他输入值相同的情况下,任何一个输入值的变化如何影响输出预测。
让我们考虑一个IT公司连续五年的员工数量和公司总营业额数据的例子。
| 员工人数 | 总营业额 |
|---|---|
| 100 | $20000 |
| 200 | $60000 |
| 300 | $100000 |
| 400 | $140000 |
| 500 | $190000 |
| 700 | ? |
上表包含员工数量和公司营业额的数据。作为一家IT公司,员工是资源,资源数量的增加将增加公司营业额。
现在公司正计划增加员工,他们想知道那一年的总营业额。在这种情况下,我们可以依靠回归分析进行最佳预测。
回归将分析输入变量(在我们的例子中是员工数量),并在变量之间建立关系,并根据这些输入变量预测连续且真实的输出。
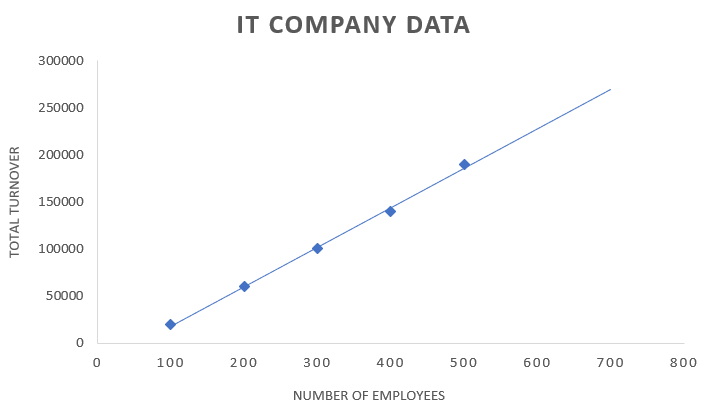
我们使用图表来显示回归,将输入和输出变量作为数据点。回归将是一条线或一条简单的曲线,它穿过此输入-输出变量图中的数据点,与数据点的距离最小。回归线与数据点之间的距离可以告诉我们模型是否获得了输入和输出变量之间的关系。
当我们理解回归分析时,我们都会在脑海中产生一个问题:我们为什么需要回归分析?在这个现代世界中,我们可以看到许多真实世界的应用,它们需要根据输入变量进行准确的连续预测,并且能够预测输入变量的变化如何影响输出预测。
让我们以股票市场为例,我们可以很容易地识别股票趋势,这有助于投资。考虑一家公司,它可以使用回归分析,利用以前的数据和变化来预测未来的市场销售额。同样,天气预报、经济预报以及许多其他应用都使用回归分析。
机器学习中我们使用了各种类型的回归,它们具有不同的特征和重要性。我们必须根据数据和我们的需求进行选择,它们是:
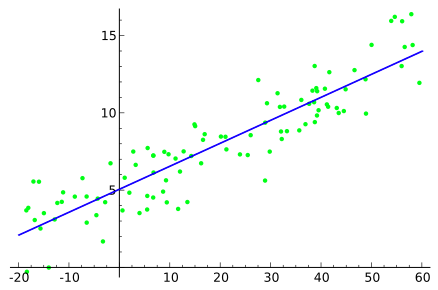
线性回归是机器学习中最基本的回归类型。它使用统计方法进行预测。线性回归包含一个输入变量(我们将其表示为线性回归图的X轴)和一个目标变量(我们将其表示为Y轴)。线性回归在回归图中绘制一条线。
在线性回归中,如果存在多个独立变量,我们称之为多元线性回归。
线性回归用方程表示:
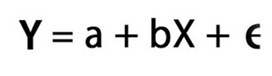
线性回归的适用性是:
逻辑回归是另一种回归分析方法,它基于概率概念工作,如果我们需要解决分类问题,我们就会使用它。这意味着逻辑回归的输出变量将是二进制值“0”或“1”。
逻辑回归处理需要分类的问题,例如真或假、是或否、垃圾邮件或非垃圾邮件等。
在逻辑回归中,我们使用 sigmoid 曲线来表示输入(独立)和输出(目标)变量之间的关系。我们将逻辑回归表示为:
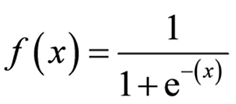
其中,
最后,我们必须提供输入变量,它们会生成一个形状曲线图。
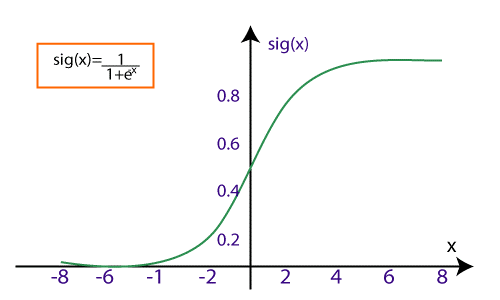
我们可以将逻辑回归分为3种类型,即:
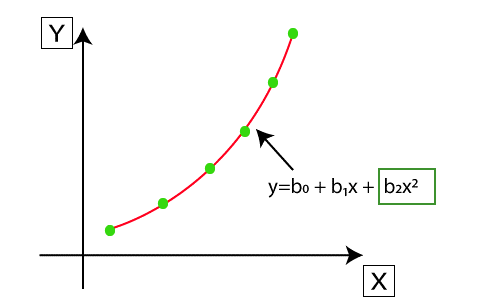
多项式回归与多元线性回归非常相似,但有一些修改。在多项式图中,输入和输出变量之间的关系将由n次表示,这意味着多项式回归由X轴和Y轴值之间的非线性曲线表示。
考虑一个数据集,其中一些数据点以非线性方式绘制在图中,在这种情况下,线性回归方法将无法正常工作。我们需要一条非线性曲线来连接所有数据点,这称为多项式回归。
在多项式回归中,真实特征被转换为具有某个次的多项式特征,我们将其称为n次,并与多项式线拟合。
我们将多项式方程表示为:
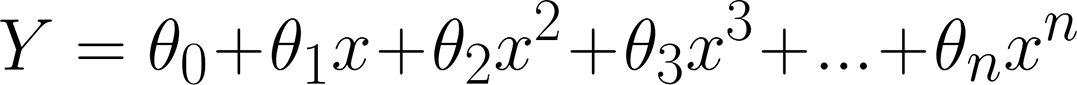
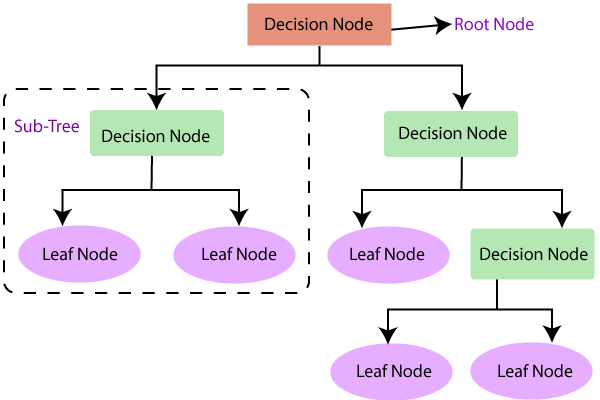
决策树回归是一种树状结构,可用于分类和回归类型。正如我们所知,决策树结构具有内部节点、分支和叶子,所有这些都用于分类和数值数据问题。
决策树结构
正如我们都知道的,它就像一个树状结构,从根数据集开始,分裂成左右子节点,代表父数据集的子集。它又分裂成它们的子节点,使它们成为父节点。下面绘制了一个决策树,以便清晰理解。
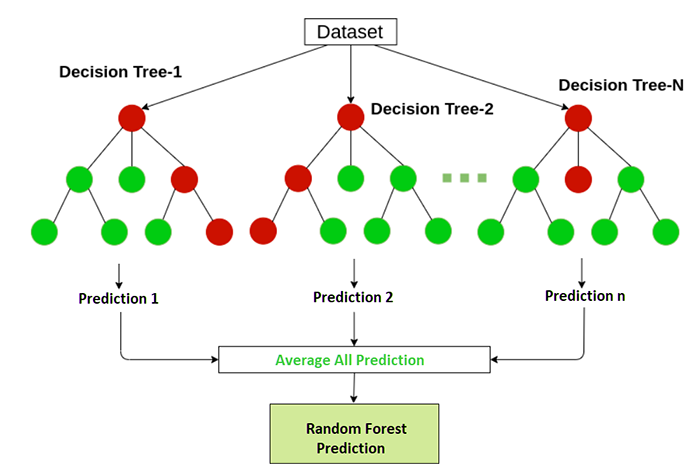
这是一种更复杂的回归方法,它结合了多个决策树回归。随机森林回归是一种非常强大的算法,可用于分类和回归任务。
随机森林回归通过结合决策树并取每棵树结果的平均值来预测输出。随机森林回归中使用的决策树被称为基础模型。随机决策树可以用公式表示:
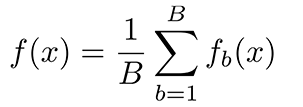
即 g(x)= f0(x)+ f1(x)+ f2(x)+....
随机森林回归有助于防止模型中称为过拟合的问题。
岭回归是一种灵活而强大的回归分析方法,当输入变量之间存在高度相关性时使用。如果共线性非常高,我们将在岭回归方法中添加一些偏差。我们添加的偏差量在岭回归中称为惩罚。岭回归对过拟合问题不太敏感。
我们可以使用以下公式表示岭回归:
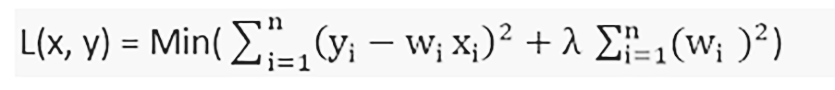
岭回归有助于解决参数数量众多且它们之间高度相关的问题。岭回归也用于降低模型的复杂性,我们称之为L2正则化。
与岭回归一样,Lasso回归也通过添加一些惩罚来降低模型的复杂性。唯一的区别是,在Lasso中我们添加的是实际的惩罚量,而在岭回归中我们使用的是惩罚量的平方。
Lasso回归可以收缩到绝对零值。Lasso回归也称为L1正则化,它表示为:
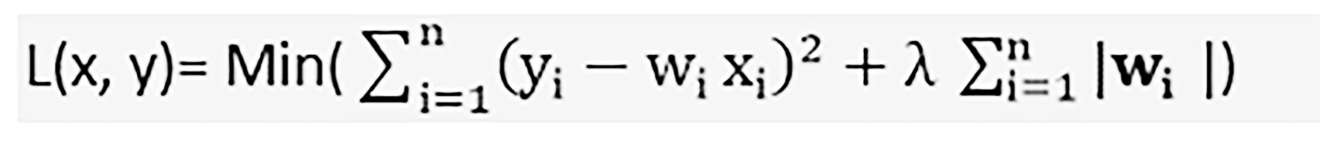
支持向量回归可用于回归和分类算法。如果将其用于回归,我们称之为支持向量回归。支持向量使用连续输入变量。
在支持向量回归中,我们试图找到一条能够到达几乎所有数据点的线,并预测称为超平面的连续变量,且具有最大边距。
支持向量回归的目标是利用超平面绘制一条边界线,覆盖最大数量的数据点。
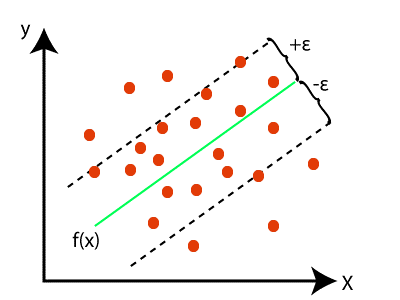
在此图中,绿线代表超平面,虚线代表相对于超平面的边界线。红点是数据点。